Help Solve a Circuit Using Mesh Current Analysis

Question

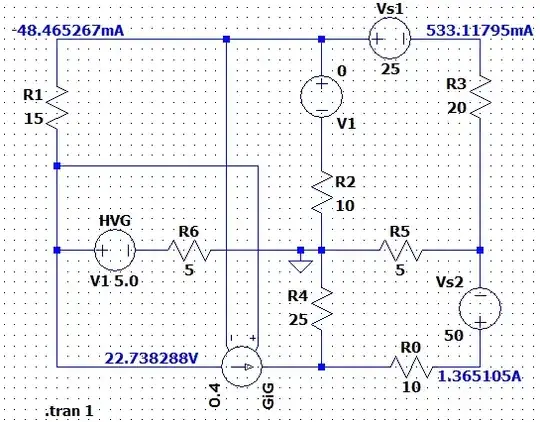
I'm Trying To Solve This Circuit Using Mesh Current Analysis But I'm getting that the currents are unsolvable (Matrix is wrong ) .

Question :

Find The Power of Each Source in :

$$ \Downarrow $$My Try At Solving This :

I Randomly Chose Current Flow Directions , Then Using Mesh Current Analysis I Got : $$\begin{aligned}\left( 1\right) I_{1}\left( R_{2}+R_{1}+R_{1}\right) +I_{2}R_{2}+I_{3}R_{6}=V_{G}\\ \left( 2\right) I_{2}\left( R_{2}+R_{3}+R_{5}\right) +I_{1}R_{2}+I_{4}R_{5}=V_{S1}\\ \left( 3\right) I_{3}\left( R_{4}+R_{6}\right) +I_{1}R_{6}+I_{4}R_{4}=V_{G}\\ \left( 4\right) I_{4}\left( R_{0}+R_{4}+R_{5}\right) +I_{3}R_{4}+I_{2}R_{5}=V_{s2}\end{aligned}$$

Using KVL for \$i_{x}\$ We Get: $$\begin{aligned}\begin{cases}i_{x}=I_{1}+I_{2}\\ V_{0}=5\cdot i_{x}=5\cdot \left( I_{1}+I_{2}\right) \end{cases}\\\end{aligned} $$ And : $$\begin{aligned}\begin{cases}V_{Y}=-I_{1}\cdot R_{1}=-15\cdot I_{1}\\ I_{3}=i_{G}=0.4\cdot V_{Y}=-6I_{1}\end{cases}\end{aligned} $$

Hence We Get :

$$ \begin{gathered}\left( 1\right) I_{1}\cdot 30+I_{2}\cdot 10+I_{1}\cdot -30 & = 5 I_{1}+I_{2}\ \\ -I_{1}\cdot 5+I_{2}5 & = 0\\ \left( 2\right) I_{1}\cdot 10+I_{2}\cdot 35+I_{4}\cdot 5-25 & =0\\ \left( 3\right) I_{1}\cdot 5-I_{1}\cdot 180+I_{4}\cdot 25 & =5\left( I_{1}+I_{2}\right) \\ -I_{1}\cdot 180-I_{2} \cdot 5 +I_{4}\cdot 25 & =0\\ \left( 4\right) -I_{1} \cdot 150+I_{2}\cdot 5+I_{4}\cdot 40-50 & =0\end{gathered}$$

A Cleaner Look : $$ \begin{gathered}\left( 1\right)-I_{1}\cdot 5+I_{2}\cdot5 & = 0\\ \left( 2\right) I_{1}\cdot 10+I_{2}\cdot 35+I_{4}\cdot 5 & =25\\ \left( 3\right)-I_{1}\cdot 180-I_{2} \cdot 5 +I_{4}\cdot 25 & =0\\ \left( 4\right) -I_{1} \cdot 150+I_{2}\cdot 5+I_{4}\cdot 40 & =50\end{gathered}$$

Yet , there is NO SOLUTION to these Set of Equations (The system is inconsistent):

$$ \begin{pmatrix} -5 & 5 & 0 &\bigm|& 0\\ 10 & 35 & 5 &\bigm|& 25 \\ -180 & -5 & 25 &\bigm|& 0\\ -150 & 5 & 40 &\bigm|& 50\\ \end{pmatrix} \longrightarrow ... \longrightarrow \begin{pmatrix} 1 & 0 & 0 &\bigm|& \frac{25}{82}\\ 0 & 1 & 0 &\bigm|& \frac{25}{82} \\ 0 & 0 & 1 &\bigm|& \frac{185}{82}\\ 0 & 0 & 0 &\bigm|& \frac{325}{82}\\ \end{pmatrix} $$

- I Really Don't know why my solution is not working , I'd Appreciate Any Kind Of Help !

Answer 1

Quick summary of your problem statement

First off, here's a labeled schematic drawn up in LTspice (free from Linear Tech):

I placed a ground at the intersection, since that's where I decided to start all of the loops you have. I then went around the loop in the direction indicated.

KVL development

My equations are:

$$\begin{align*} i_G&=i_3=0.4\,i_1 R_1 \\ V_G &= 5\left(i_1+i_2\right) \\ 0\:\text{V}-R_6\left(i_1+i_3\right)+V_G-R_1\, i_1-R_2\left(i_1+i_2\right)&=0\:\text{V} \\ 0\:\text{V}-R_5\left(i_2+i_4\right)-R_3\, i_2+V_{S_1}-R_2\left(i_2+i_1\right)&=0\:\text{V} \\ 0\:\text{V}-R_6\left(i_3+i_1\right)+V_G+V_{i_{_\text{G}}}-R_4\left(i_3+i_4\right)&=0\:\text{V} \\ 0\:\text{V}-R_5\left(i_4+i_2\right)+V_{S_2}-R_0\, i_4-R_4\left(i_4+i_3\right)&=0\:\text{V} \end{align*}$$

I assigned a voltage across the dependent current source, of course, to solve for. And note the sign for \$i_3\$ that I used. It's different from what I saw in your question.

Solver solution

Using SymPy, I find:

var('r0 r1 r2 r3 r4 r5 r6 i1 i2 i4 vs1 vs2 vig')
vg = 5 * ( i1 + i2 )
i3 = 0.4 * i1 * r1
eq1 = Eq( 0 - r6*(i1+i3) + vg - r1*i1 - r2*(i1+i2), 0 )
eq2 = Eq( 0 - r5*(i2+i4) - r3*i2 + vs1 - r2*(i2+i1), 0 )
eq3 = Eq( 0 - r6*(i3+i1) + vg + vig - r4*(i3+i4), 0 )
eq4 = Eq( 0 - r5*(i4+i2) + vs2 - r0*i4 - r4*(i4+i3), 0 )
ans = solve( [ eq1, eq2, eq3, eq4 ], [ i1, i2, i4, vig ] )

ans[ i1 ].subs({r0:10,r1:15,r2:10,r3:20,r4:25,r5:5,r6:5,vs1:25,vs2:50})
     -0.0484652665589661
ans[ i2 ].subs({r0:10,r1:15,r2:10,r3:20,r4:25,r5:5,r6:5,vs1:25,vs2:50})
      0.533117932148627
ans[ i4 ].subs({r0:10,r1:15,r2:10,r3:20,r4:25,r5:5,r6:5,vs1:25,vs2:50})
      1.36510500807754
ans[ vig ].subs({r0:10,r1:15,r2:10,r3:20,r4:25,r5:5,r6:5,vs1:25,vs2:50})
      22.7382875605816

That's what I get for answers.

Comparison vs Spice simulation

Here's what LTspice says:

I think that's a match.

Summary

It's now your job to examine your own development and compare it with what I did.

Keep in mind that you can construct, out of whole cloth, voltage differences and currents where you need them. In this case, as I was walking around the loop for \$i_3\$ I found I needed a "voltage difference" for the dependent current source. So I just made one up on the spot.

As you can see, it either works out (as it should for a problem you are given) or else it doesn't because you've either over-specified or under-specified the problem. In this case, it worked out fine because the problem is, in fact, solvable. Which is a good thing.

Answer 2

Your equation 3 doesn't include a term for the dependent current source, \$i_G\$. You can't just ignore the voltage across that source or assume that it is zero.