3

This question is motivated by an automotive problem from this question.

In a quad vehicle, in a 12V system, there's a fuel sender with 0-100 ohm range, empty to full. The fuel sender was a part of a retrofit fuel cell assembly and cannot be easily replaced.

Now, the electronic control unit (ECU) expected the original fuel sender to provide 450-100 ohm resistance, empty to full.

The problem is thus: how to map the resistance from the 0-100 ohm sender to synthesize a virtual impedance for the ECU, in the range it expects. I.e. a mapping (0->450, 100->100).

The ECU has a ground-referenced sensing circuit: it keeps one end of the resistance at a fairly low voltage, drives the other end from a current source or a resistor, and uses the voltage thus developed across the fuel sender - in our case a virtual one.

Kuba hasn't forgotten Monica
  • 32,734
  • 1
  • 38
  • 103
  • 2
    *and uses the voltage thus developed across the fuel sender* - why not just overpower that voltage with the appropriate value based on a regular amplifier? – Andy aka Apr 18 '22 at 23:32
  • 1
    you could make a fake fuel sender by the use of a microcontroller with a digitally controlled resistor, or with a stepping motor and a potentiometer – jsotola Apr 18 '22 at 23:41
  • 2
    @Andyaka We don't know what current or resistance the ECU uses to sense the fuel sender. It expects a resistor, so whatever we put there has to act like one. And the MCU is of course a very practical solution, and can be cheaply and easily made to do the job perfectly. But to me personally that's not as enjoyable as figuring an analog solution, ideally one that uses boring non-special parts. – Kuba hasn't forgotten Monica Apr 19 '22 at 04:49
  • 1
    " We don't know what current or resistance the ECU uses to sense the fuel sender." It could be measured. The poster of the original question has asked for an electronic solution so is presumably capable of taking some current or voltage readings from the sensor connection. It should then be simpler to implement @Andyaka's suggestion of injecting the corresponding voltage than providing an electronically generated resistance, notwithstanding the ingenuity of your circuits. – Graham Nye Apr 20 '22 at 11:23
  • @josotola "a stepping motor and a pot" I speculated about an RC servo and a dual gang pot (one gang for feedback and the other for the sensor input). The problem with these approaches is that the application is for an off-road vehicle so there will be high levels of shock and vibration. An all-electronic solution will be more robust. – Graham Nye Apr 20 '22 at 11:32
  • 1
    There are audio volume/fade potentiometers with built in motors. Cost a couple bucks each for the Chinese version of the Alps product. The servo to map the ranges would be a classic op-amp based circuit with hysteresis. Wonderfully clunky and old school, harkening to analog computer days. Definitely something I would love to see on a farm – with utmost respect for the creativity and can-do abilities of farmers without whom we’d all starve :) – Kuba hasn't forgotten Monica Apr 20 '22 at 21:54

1 Answers1

5

There are many approaches, but I've explored two.

Negative Impedance Converter

OA1 mirrors the R1's voltage drop around the connection point of R1 and R4, effectively negating R1's resistance. OA2 adds this impedance to 450 ohms, and synthesizes it using M1. RPOS and RNEG are the terminals of the virtual resistor.

RNEG can be up to about 5V above the ground. LM324 works fine in this application, as do other op-amps whose input common mode extends to negative supply.

The usual negative impedance converter topology cannot be directly applied, since it terminates the load in the op-amp output. Here, we need both RPOS and RNEG to be free-floating.

V1 and V2 are used for simulation of the effects of op-amp offset.

schematic

simulate this circuit – Schematic created using CircuitLab

This circuit has some non-idealities, and can be configured in one of the modes below:

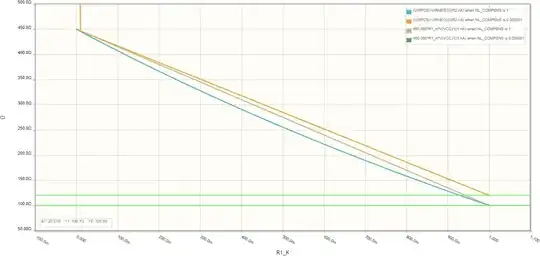
  1. Uncompensated L_COMPENS=0, NL_COMPENS=1e-6: The transfer curve has a slope error, such that the 100 ohm endpoint is raised by R_SENSE.

  2. Linearly compensated L_COMPENS=1, NL_COMPENS=1e-6: The transfer curve has nominal slope, but flattens out a bit before reaching the en.

  3. Non-linearly compensated L_COMPENS=0, NL_COMPENS=1: The transfer curve has accurate endpoints, but its midpoint is lowered by approximately R_SENSE.

  4. Not captured in the schematic is an ideal mode, which suffers none of the tradeoffs of the three modes above. A resistance divider can be used to reduce the effective resistance of R1 by a factor R_SENSE/100 ohm. The cost is an additional op-amp, mosfet, and some assorted discretes.

The transfer curves of the uncompensated linear mode (orange) and nonlinearly compensated mode (blue) against the ideal transfer curve are shown below. The green cursor lines denote the error caused by the sense resistance R_SENSE.

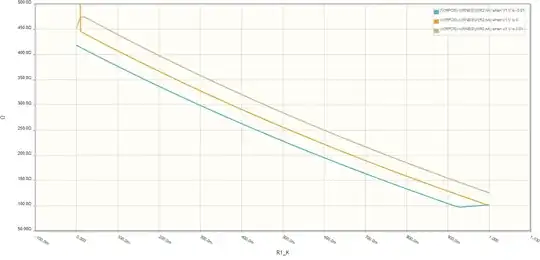
enter image description here

The transfer curve of the uncompensated linear mode (orange) against the linearly compensated mode (blue) is shown below.

enter image description here

Given the application's accuracy needs of about +/-5%, the circuit will work with 1% resistors, and optional trim of the op-amp offset voltages. It is most sensitive to the op-amp offsets. The +/-10mV maximum offset of a low-grade LM324 across temperature affects the transfer curve as follows.

For OP1:

enter image description here

For OP2:

enter image description here

The next largest error source is the nominal value of the R1 rheostat. The 5% error bounds are as follows:

enter image description here

The remaining resistors' 1% tolerances have a commensurate effect, i.e. they introduce at most 1% of error.

The circuit can be readily adapted for bipolar operation, high-side operation, etc.

Reciprocal Resistance Converter

This was my initial approach.

First, a bridge-based resistance multiplier, similar in principle to that one, is used to multiply the 100 ohm fuel gage resistance by a factor of 200x. This virtual input resistance is presented across the MPOS and MNEG nodes.

Then, a bridge-based resistance transformer maps the input resistance range to the output resistance range, presented across the RPOS and RNEG nodes.

With R1 set to 0 ohms, the R_K factor is adjusted to get desired "empty" resistance at the output. Then, with R1 set to 100 ohms, the R_TOT factor is adjusted to get the desired "empty" resistance at the output.

schematic

simulate this circuit

LM324 is used only as an example, since its input common mode includes the ground rail, as needed in this circuit. Since relatively low currents are driven through the output resistance, a 5V rail-to-rail op-amp would be sufficient, with a suitably regulated power supply.

The transfer curve is as shown below. It is not linear.

The nonlinear transfer curve of the resistance transformer

Further development of this scheme would improve the output bridge to be more linear, and/or add a nonlinear element to "bend" the 100 ohm input resistance to linearize the response.

This nonlinear response maps some float assemblies rather better than a linear fit would. The inflection of this curve can be easily inverted as well (upside down).

Kuba hasn't forgotten Monica
  • 32,734
  • 1
  • 38
  • 103