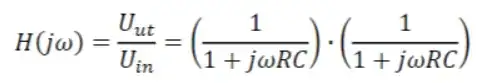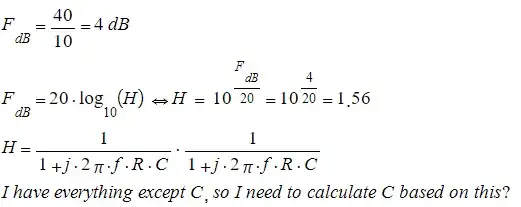The task is to make a 2:degree filter with a slope of 40 dB/decade.
I have this circuit. R1=R2=10kΩ, f=1kHz
I also have this formula
What I think (probably wrong). Is that that because
40 dB/decade, then
I'm not quite sure that I have gotten the decibel conversion (to H) right. But if that is right, how do I calculate the value of C when there is that imaginary j in the expression?
The magnitude of H is:
Your equation is the transfer function correctly of two cascaded RC low pass filters with a buffer in between them so there is very little loading effect on the first filter by the second filter.
You need to find the magnitude of the transfer function so, first get it in the form a+jb, then find the magnitude from sqrt(a^2 + b^2). Equate the expression for the magnitude of the transfer function to 0.707 which is the magnitude at the -3dB frequency then transpose to make C the subject of the equation.
Well, in this answer I showed that the formula to find the slope (in dB/decade) is given by:
$$\mathcal{I}\left(\omega\right)=20\log_{10}\left(\lim_{\omega\to\infty}\frac{\left|\underline{\mathscr{H}}\left(10\omega\text{j}\right)\right|}{\left|\underline{\mathscr{H}}\left(\omega\text{j}\right)\right|}\right)\tag1$$
Now, in your case we have:
$$\left|\underline{\mathscr{H}}\left(\omega\text{j}\right)\right|=\frac{1}{1+\left(\text{CR}\omega\right)^2}\tag2$$
So, we get:
$$\frac{\left|\underline{\mathscr{H}}\left(10\omega\text{j}\right)\right|}{\left|\underline{\mathscr{H}}\left(\omega\text{j}\right)\right|}=\frac{\frac{1}{1+\left(10\text{CR}\omega\right)^2}}{\frac{1}{1+\left(\text{CR}\omega\right)^2}}=\frac{1+\left(\text{CR}\omega\right)^2}{1+\left(10\text{CR}\omega\right)^2}=\frac{\frac{1}{\omega^2}+\left(\text{CR}\right)^2}{\frac{1}{\omega^2}+\left(10\text{CR}\right)^2}\tag3$$
Taking the limit gives:
$$\lim_{\omega\to\infty}\frac{\frac{1}{\omega^2}+\left(\text{CR}\right)^2}{\frac{1}{\omega^2}+\left(10\text{CR}\right)^2}=\frac{0+\left(\text{CR}\right)^2}{0+\left(10\text{CR}\right)^2}=\frac{1}{10^2}=\frac{1}{100}\tag4$$
And, so you get:
$$\mathcal{I}\left(\omega\right)=20\log_{10}\left(\frac{1}{100}\right)=-40\space\text{dB/decade}\tag5$$
EDIT:
In order to find the cut-off frequency we can use:
$$\left|\underline{\mathscr{H}}\left(\omega_0\text{j}\right)\right|=\frac{1}{\sqrt{2}}\tag6$$
When solving this you will find:
$$\text{C}=\frac{\sqrt{\sqrt{2}-1}}{\text{R}\omega_0}=\frac{\sqrt{\sqrt{2}-1}}{2\pi\text{Rf}_0}\tag7$$
Using your values, you'll find:
$$\text{C}=\frac{\sqrt{\sqrt{2}-1}}{2\pi\cdot10\cdot1000\cdot1\cdot1000}=\frac{\sqrt{\sqrt{2}-1}}{20000000\pi}\approx1.024312\cdot10^{-8}\space\text{F}\tag8$$
