I can't wrap my head around how the SR Latch works. Seemingly, you plug an input line from R, and another from S, and you are supposed to get results in Q and Q′.
However, both R and S require input from the other's output, and the other's output requires input from the other other's output. What comes first the chicken or the egg??
When you first plug this circuit in, how does it get started?
A perceptive question. In fact, if you build this latch in a simulation program, it will indeed show you that it can't predict what state it will start in:
But if you set one of the inputs high (those are pushbuttons on the left), the signal will propagate through (remember, 1 OR [anything] equals 1) and the circuit will latch that state:
These are NOR gates, so the inverted output goes low when either input is high. The program I used is Logisim. It is small, and I recommend it for starting out. Logic compilers (FPGA and everything else) love to complain about uninitialized states. This was a great first example.
Now, I know that in real life, the circuit will randomly latch into one or the other state on its own. Many others have pointed that out. But sometimes, it's important that it reliably start in one state or another, and that's what all the warnings are about.
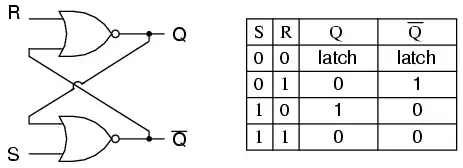
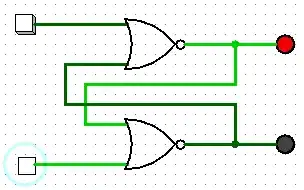
A flip-flop is implemented as a bi-stable multivibrator; therefore, Q and Q' are guaranteed to be the inverse of each other for all inputs except S=1, R=1, which is not allowed. The excitation table for the SR flip-flop is helpful in understanding what occurs when signals are applied to the inputs.
S R Q(t) Q(t+1)
----------------
0 x 0 0
1 0 0 1
0 1 1 0
x 0 1 1
The outputs Q and Q' will rapidly change states and come to rest at a steady state after signals have been applied to S and R.
Example 1: Q(t) = 0, Q'(t) = 1, S = 0, R = 0.
State 1: Q(t+1 state 1) = NOT(R OR Q'(t)) = NOT(0 OR 1) = 0
Q'(t+1 state 1) = NOT(S OR Q(t)) = NOT(0 OR 0) = 1
State 2: Q(t+1 state 1) = NOT(R OR Q'(t+1 state 1)) = NOT(0 OR 1) = 0
Q'(t+1 state 2) = NOT(S OR Q(t+1 state 1)) = NOT(0 OR 0) = 1
Since the outputs did not change, we have reached a steady state; therefore, Q(t+1) = 0, Q'(t+1) = 1.
Example 2: Q(t) = 0, Q'(t) = 1, S = 0, R = 1
State 1: Q(t+1 state 1) = NOT(R OR Q'(t)) = NOT(1 OR 1) = 0
Q'(t+1 state 1) = NOT(S OR Q(t)) = NOT(0 OR 0) = 1
State 2: Q(t+1 state 2) = NOT(R OR Q'(t+1 state 1)) = NOT(1 OR 1) = 0
Q'(t+1 state 2) = NOT(S OR Q(t+1 state 1)) = NOT(0 OR 0) = 1
We have reached a steady state; therefore, Q(t+1) = 0, Q'(t+1) = 1.
Example 3: Q(t) = 0, Q'(t) = 1, S = 1, R = 0
State 1: Q(t+1 state 1) = NOT(R OR Q'(t)) = NOT(0 OR 1) = 0
Q'(t+1 state 1) = NOT(S OR Q(t)) = NOT(1 OR 0) = 0
State 2: Q(t+1 state 2) = NOT(R OR Q'(t+1 state 1)) = NOT(0 OR 0) = 1
Q'(t+1 state 2) = NOT(S OR Q(t+1 state 1)) = NOT(1 OR 0) = 0
State 3: Q(t+1 state 3) = NOT(R OR Q'(t+1 state 2)) = NOT(0 OR 0) = 1
Q'(t+1 state 3) = NOT(S OR Q(t+1 state 2)) = NOT(1 OR 1) = 0
We have reached a steady state; therefore, Q(t+1) = 1, Q'(t+1) = 0.
Example 4: Q(t) = 1, Q'(t) = 0, S = 1, R = 0
State 1: Q(t+1 state 1) = NOT(R OR Q'(t)) = NOT(0 OR 0) = 1
Q'(t+1 state 1) = NOT(S OR Q(t)) = NOT(1 OR 1) = 0
State 2: Q(t+1 state 2) = NOT(R OR Q'(t+1 state 1)) = NOT(0 OR 0) = 1
Q'(t+1 state 2) = NOT(S OR Q(t+1 state 1)) = NOT(1 OR 1) = 0
We have reached a steady state; therefore, Q(t+1) = 1, Q'(t+1) = 0.
Example 5: Q(t) = 1, Q'(t) = 0, S = 0, R = 0
State 1: Q(t+1 state 1) = NOT(R OR Q'(t)) = NOT(0 OR 0) = 1
Q'(t+1 state 1) = NOT(S OR Q(t)) = NOT(0 OR 1) = 0
State 2: Q(t+1 state 2) = NOT(R OR Q'(t+1 state 1)) = NOT(0 OR 0) = 1
Q'(t+1 state 2) = NOT(S OR Q(t+1 state 1)) = NOT(0 OR 1) = 0
We have reached a steady; state therefore, Q(t+1) = 1, Q'(t+1) = 0.
With Q=0, Q'=0, S=0, and R=0, an SR flip-flop will oscillate until one of the inputs is set to 1.
Example 6: Q(t) = 0, Q'(t) = 0, S = 0, R = 0
State 1: Q(t+1 state 1) = NOT(R OR Q'(t)) = NOT(0 OR 0) = 1
Q'(t+1 state 1) = NOT(S OR Q(t)) = NOT(0 OR 0) = 1
State 2: Q(t+1 state 2) = NOT(R OR Q'(t+1 state 1)) = NOT(0 OR 1) = 0
Q'(t+1 state 2) = NOT(S OR Q(t+1 state 1)) = NOT(0 OR 1) = 0
State 3: Q(t+1 state 3) = NOT(R OR Q'(t+1 state 2)) = NOT(0 OR 0) = 1
Q'(t+1 state 3) = NOT(S OR Q(t+1 state 2)) = NOT(0 OR 0) = 1
State 4: Q(t+1 state 4) = NOT(R OR Q'(t+1 state 3)) = NOT(0 OR 1) = 0
Q'(t+1 state 4) = NOT(S OR Q(t+1 state 3)) = NOT(0 OR 1) = 0
...
As one can see, a steady state is not possible until one of the inputs is set to 1 (which is usually handled by power-on reset circuitry).
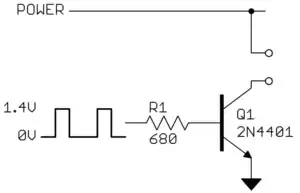
If we examine simplest implementation of an SR flip-flop (see http://en.wikipedia.org/wiki/File:Transistor_Bistable_interactive_animated_EN.svg), we discover that it is composed of two bi-polar junction transistors (BJTs) and four resistors (replace the SPST toggle switches to ground with SPDT switches that can switch the set and reset lines between ground potential and V+). The BJTs are configured as common emitter inverters. The collector (output) of each transistor is fed back into the base (input) of the opposite transistor. The input S is wire-ORed with the output of the BJT whose collector connection serves as the output Q (the junction of R1/R3). The input R is wire-ORed with the output the BJT whose collector connection serves as the output Q' (the junction of R2/R4).
When the circuit first powers up, neither transistor is forward-biased into the saturation region for a tiny fraction of a second, which means that both Q and Q' are at logic level 1. The voltage available at each collector is fed to the base of the opposite transistor, which causes it to become forward biased into the saturation region. The transistor that becomes forward-biased first will start conducting current first, which, in turn, will cause a voltage drop to occur across its collector resistor, setting its output to logic level 0. This drop in collector voltage will prevent the opposite transistor from becoming forward-biased; therefore, setting the initial state of the flip-flop. It’s basically a hardware race condition that leads to an unpredictable outcome.
Like you said, it's undefined. In practice there are transients or quirks which should put the latch into a certain state, but there is no guarantee which state it will be in. This is caused by mismatched in the two gates which will define a given initial state (basically the circuit doesn't behave as a true digital SR latch but is a complex analog circuit as it is in real life). The initial output will be more or less random, either Q=1 and ~Q=0 or Q=0 and ~Q=1.
Barring explicit mention by a datasheet I would not rely on one state being chosen over the other as the actual init state can change between different parts in the batch, placement on a board, environmental factors (temperature/humidity/etc.), and aging (by no means a complete list of factors).
The best way to define a state is after startup assert either the set or reset to put the SR latch into a known state.
As a side note, in general SR latches asserting S and R at the same time will also result in undefined behavior and you're relying on similar voodoo to set the outputs (a real implementation may shut off both outputs, randomly toggle the two, toggle both outputs on, etc.). As supercat commented if one pin is unasserted before the other the SR latch can enter a known state because only one pin is being asserted. Other types of latches/flip flops may define a different behavior, for example JK flip-flops define asserting both pins to toggle the outputs (Q = ~Qprev, ~Q = Qprev).
Keep in mind that the gates are inverting. This provides a positive feedback loop. Assuming that both S and R are zero and one output is one, this one will feed back into the other gate to force the other output to zero. This way, the gates are in either of two stable states.
As soon as you set one of S or R to one, this will force the corresponding gate to output zero which, in turn, will force the other gate to output zero. Again, stable.
For example, initial state: S = 0, R = 0, Q = 0, Q# = 1. You now set S = 1. This will change the lower gate output (Q#) to 0. This 0 feeds into the upper gate, forcing that output (Q) to 1. This 1 feeds back to the lower gate. When you set S back to 0, the lower gate is still receiving the 1 from the other gate. This will keep the Q# output at 0.
If Q already is 1 and you set S to 1, both inputs to the lower gate are 1 and so there is no change.
I think the important bit that you are asking about has to do with the fact that the latch powers up in an unknown state, so how do we ever get it into a known state. You need to remember that if either input to a NOR gate is a 1 then the output must be a 0, regardless of the state of the other input. So applying the SET or RESET input combinations will always force the latch into the set or reset state, regardless of the previous state of the latch.
