I have a complicated electrical network. I would like to calculate voltage drop across across the network i.e. nodes 2-15, given V1=10 V and V16=0 V. The values of the resistances are known.
Is there a Python package which can calculate? I can write equation for each node using Ohm's and Kirchoff's laws, but then manually solving 14 linear equations simultaneously is tedious.
I'll follow the algorithm and benchmark problem from this answer.
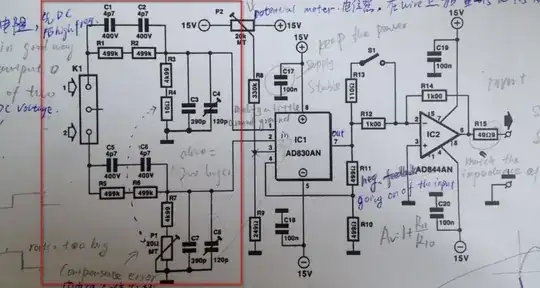
simulate this circuit – Schematic created using CircuitLab
The code is dirty and does the job. It could be much improved, but I had no time to further mess with it.
import random
class Item:
def __new__(cls, n: int):
if n in cls.all:
return cls.all[n]
item = super().__new__(cls)
item.n = n
cls.all[n] = item
return item
class Node(Item):
all = {}
def __init__(self, n: int):
super().__init__()
if not hasattr(self, 'elements'):
self.elements = {}
self.adjacentNodes = {}
self.adjacentElements = {} # indexed by nodes
def __iadd__(self, *elements):
for el in elements:
assert isinstance(el, Element)
el.addNode(self)
self.elements[el.n] = el
def __repr__(self):
return f"{self.__class__.__name__}({self.n})"
class Element(Item):
nmax = 0
all = {}
@staticmethod
def newNumber():
Element.nmax += 1
return Element.nmax
def __new__(cls, *nodeNumbers, n: int|None=None, **kwargs):
return super().__new__(cls, n or Element.newNumber())
def __init__(self, *nodeNumbers, **kwargs):
super().__init__()
if not hasattr(self, 'nodes'):
self.nodes = set()
nodes = [Node(n) for n in nodeNumbers]
for node in nodes:
node += self
assert len(nodes) in [0,2]
if nodes:
nodes[0].adjacentNodes[nodes[1].n] = nodes[1]
nodes[0].adjacentElements[nodes[1].n] = self
nodes[1].adjacentNodes[nodes[0].n] = nodes[0]
nodes[1].adjacentElements[nodes[0].n] = self
return True
return False
def addNode(self, node):
self.nodes.add(node)
class R(Element):
def __init__(self, *args, r=None, **kwargs):
super().__init__(*args, **kwargs)
if not hasattr(self, 'r'):
if r is None:
r = R.randomResistance()
self.r = r
@staticmethod
def randomResistance(min=0.1, max=1E3):
return min + random.betavariate(alpha=2, beta=5)*max
def __repr__(self):
return f"{self.__class__.__name__}({self.n}: r={self.r} {self.nodes})"
# define the problem
if 0:
# The problem from the question
R(1, 2), R(2, 3), R(1, 4), R(2, 5), R(3, 6)
R(4, 5), R(5, 6), R(4, 7), R(5, 8), R(6, 9)
R(7, 8), R(8, 9), R(9, 10), R(8, 11), R(9, 12), R(10, 13)
R(11, 12), R(12, 13), R(11, 14), R(12, 15), R(13, 16)
Node(1).V = 10
Node(16).V = 0
else:
# The benchmark problem
R(1, 2, n=7, r=5), R(2, 3, n=8, r=21)
R(1, 4, n=1, r=61), R(2, 5, n=2, r=50), R(3, 6, n=3, r=16)
R(4, 5, n=10, r=76), R(5, 6, n=9, r=10)
R(4, 7, n=4, r=56), R(5, 8, n=5, r=45), R(6, 9, n=6, r=18)
R(7, 8, n=11, r=32), R(8, 9, n=12, r=22)
Node(4).V = 0
Node(6).V = 1
# determine the parallel resistance of attached resistors
for node in Node.all.values():
rpar = 0
for el in node.elements.values():
rpar += 1/el.r
node.rpar = 1/rpar
# determine the computation order
nodeOrder = []
nodes = {}
for n, node in Node.all.items():
if not hasattr(node, 'V'):
nodes[n] = node
while nodes:
remove = set()
for node in nodes.values():
for el in node.elements.values():
for depnode in el.nodes:
remove.add(depnode.n)
remove.remove(node.n)
group = list(set(nodes.keys()) - remove)
assert group
nodeOrder += group
for done in group:
del nodes[done]
assert not nodes
# preset node potentials
for node in Node.all.values():
if not hasattr(node, 'V'):
node.V = 0
# update node potentials
nodeOrder = [Node(n) for n in nodeOrder]
for i in range(0, 100):
for node in nodeOrder:
V = 0
for adjNode in node.adjacentNodes.values():
V += adjNode.V/node.adjacentElements[adjNode.n].r
node.V = V*node.rpar
for n in Node.all.values():
print(n.V)
The node voltages for the benchmark problem are, in order 1-9:
>>> %Run rsolver.py
0.6517578962898488
0.7051806746742627
0.8725105620201647
0
0.8410039648620072
1
0.47455268117334604
0.7457256418438295
0.8855765388295932
They match with the CircuitLab simulation results.
