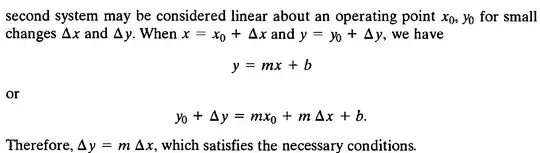1

It is not clear to me how he goes to the conclusion.

enter image description here

enter image description here

Ali
  • 25
  • 4
  • 2
    The +b part makes superposition not work. If you double x, y does not double unless b is zero. – DKNguyen Feb 13 '22 at 20:45
  • but the author considers it as linear about an operating point. This point is not clear to me. – Ali Feb 13 '22 at 20:47
  • That's just normal. Maybe you haven't run into yet? Linear approximations? Take any continuous function and you can find it's derivative at any point on the curve. That derivative is the slope of the straight line tangent to that point on the curve. As long as you deviate to the left or right on the X-axis by a small enough amount from that point then the Y value you get if you just followed the tangent line is about the same as what you would get from the actual function. – DKNguyen Feb 13 '22 at 20:48
  • In other words, the reason you can often just think of the Earth's surface as flat is because in those instances you are only interacting with only a very small part of a very large sphere. – DKNguyen Feb 13 '22 at 20:52
  • For the system "y=mx+b", the approximation that @DKNguyen mentioned isn't even an approximation: It holds for an arbitrarily large delta-x. This means that superposition still works in a limited fashion: You can compute delta-y from delta-x using superposition. That, in turn, means that you can "translate" the original not-technically-linear system into a linear system (of deltas), making it "effectively linear". Or "linear enough to use superposition with some caution about that +b term". – Jonathan S. Feb 13 '22 at 21:00
  • @DKNguyen I have taken linear approximation. I think we do not approximate linear equations. Still sorry, not clear – Ali Feb 13 '22 at 21:13
  • You're conflating being a line with linearity (which means superposition works). Using a linear approximation on y=mx+b allows you to use it with linear combinations (superposition). – DKNguyen Feb 13 '22 at 21:22

1 Answers1

1

It says specifically that "a system represented by the relation \$y=mx+b\$ is not linear".

But then he shows that for this system, if we consider perturbations about the operating point, then equations that describe the response to those perturbations is \$\Delta y = m\Delta x\$. And this is a linear relation.

The Photon
  • 126,425
  • 3
  • 159
  • 304