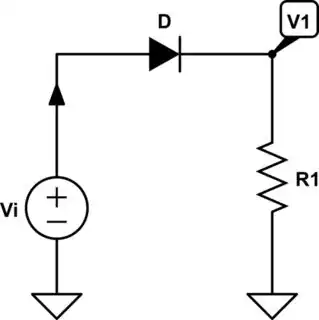
It is given that
\$V_i=u\sin(\omega t +\varphi)\$
and
\$I_D=I_S \left[ \exp \left( \frac{qV_D}{\eta k T} \right)-1 \right]\$
From the circuit, we can say:
\$V_1 = V_i-V_D\$
and
\$I_D=\frac{V_1}{R_1}\$
So, we get:
\$\frac{V_1}{R_1}=I_S \left[ \exp \left( \frac{qV_D}{\eta k T} \right)-1 \right]\$
\$\Rightarrow \frac{V_1}{R_1I_S}= \exp \left( \frac{qV_D}{\eta k T} \right)-1\$
Defining \$C_1 := \frac{1}{R_1I_S}\$ and \$C_2:=\frac{q}{\eta k T}\$, we get
\$C_1V_1= \exp \left( C_2V_D \right)-1\$
\$\Rightarrow \frac{V_1}{C_1}+1=\exp(C_2V_D)\$
\$\Rightarrow \ln \left( \frac{V_1}{C_1}+1 \right)=C_2V_D\$
\$\Rightarrow V_D = \frac{1}{C_2} \ln \left( \frac{V_1}{C_1}+1 \right)\$
Hence voltage relation can be re-written as:
\$V_1 = V_i - \frac{1}{C_2} \ln \left( \frac{V_1}{C_1}+1 \right)\$
\$\Rightarrow C_2V_1 = C_2V_i - \ln \left( \frac{V_1}{C_1}+1 \right)\$
\$\Rightarrow \ln \left( \frac{V_1}{C_1}+1 \right) = C_2V_i - C_2V_1 \$
\$\Rightarrow \frac{V_1}{C_1}+1 = \exp \left( C_2V_i - C_2V_1 \right) \$
\$\Rightarrow \frac{V_1}{C_1}+1 = \exp \left( C_2V_i \right) \exp \left(- C_2V_1 \right) \$
\$\Rightarrow \frac{V_1}{C_1} = \exp \left( C_2V_i \right) \exp \left(- C_2V_1 \right) -1 \$
\$\Rightarrow V_1 = C_1\exp \left( C_2V_i \right) \exp \left(- C_2V_1 \right) - C_1 \$
The general solution using Lambert W function is given by (see Wikipedia for quick reference and a book for compelte reference):
\$x = a+b\exp \left( cx \right) \Rightarrow x=a-\frac{1}{c}W \left( -bc\exp(ac) \right)\$
Using the above solution considering \$V_1=x\$, \$a= -C_1\$, \$b=C_1\exp(C_2V_i)\$, and \$c=-C_2\$, we obtain
\$V_1=-C_1+\frac{1}{C_2}W \left( C_1C_2\exp(C_2V_i) \exp(C_1C_2) \right)\$
And hence:
\$V_1=-C_1+\frac{1}{C_2}W \left( C_1C_2\exp(C_2u\sin(\omega t +\varphi)) \exp(C_1C_2) \right)\$