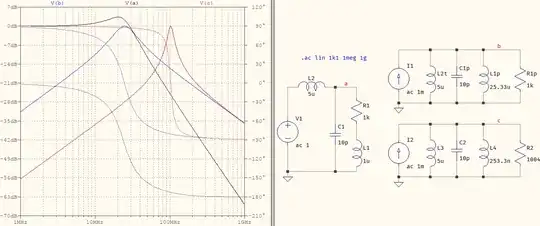
It can't be done that way unless you want it to be calculated at a fixed frequency, only. Otherwise, if you look at the first circuit, L2 and C1 form a lowpass (with a series RL as a load), while the second circuit is the equivalent of an L||C (with a resistive load, damping), which is a bandpass. Series to parallel transformations, and vice-versa, rely on the reactance, thus defined at a single frequency.
In the comment below, @jonk is right: some explanation is needed for the opening phrase.
That quality factor you mention has only a meaning for the simple 2nd order circuit and, in your case, its expression signifies the damping (there is more than one meaning). That can be achieved in your 2nd picture: the two inductances can be merged, leaving the parallel RLC. But its expression, then, will be particular to that topology. An LC lowpass (the kind that you have in your 1st picture) will have its own, and even then it only has meaning as long as the transfer function is a 2nd order. But the 1st picture is more complex than that, becaue the load is not purely resistive -- it's a complex impedance in the form of \$R+jX_L\$. And that makes the transfer function of the 1st circuit to become:
$$H_1(s)=\dfrac{1}{L_2C_1}\dfrac{s+\dfrac{R_1}{L_1}}{s^3+\dfrac{R_1}{L_1}s^2+\dfrac{1}{(L_1||L_2)C_1}s+\dfrac{R_1}{L_1L_2C_1}} \tag{1}$$
The 2nd one is the banal 2nd order bandpass. Overall, this is a 3rd order transfer function, even if the \$s\$ in the numerator means there is a zero that will cancel one pole. But the denominator can now be factored as two polynomials: a 2nd order and a 1st order. To make things more difficult, the meaning of Q is ambiguous now. Which one would you consider: the Q of the LC lowpass, or the Q of the series RL load? In fact, what's stopping you from considering the RLC circuit formed by R1, L1, C1? That, too, will have its own quality factor. These two have different meanings: the 1st is related to the damping of the pole, while the 2nd relates to the efficiency, or the "purity" of the inductor, or capacitor (real LC elements never have a pure 20 dB/dec slope).
And the meanings do not stop here, as you've seen in @LvW's answer (you can also see the Wikipedia article), but it would probably diverge a bit from the goal. I will add, though, that the part where I said "...at a fixed frequency, only." referred to the series-parallel equations, where Q is defined as \$Q_s=X_s/R_s\$, or \$Q_p=R_p/X_p\$. But this is only valid for the simple impedances in the form of \$R+jX\$, and has nothing to do with a 2nd order system.
But the reason I skipped over these is because I wanted to show you that there's no need to complicate and simply evaluate, visually, what you have and what you want it to become: there are two schematics with two very different topologies. In fact, your final sentence:
My next step is to simulate both circuits to see if the frequency response for the voltage across C1 is the same...
would have been more than enough to make you realize, for yourself, why the goal is not possible. Even if it would not have been clear enough from a visual inspection of the circuit, a simulation would have immediately revealed why that transformation is not possible. I suppose one of the hidden messages is to not be afraid of the simulators, they can often bring that "...oh!" moment.
I'd like to clarify one thing. The quality factor, Q, has a universal meaning: it represents the amount of damping of the poles or zeroes. This definition is universal and can be used anywhere, even for 1st order systems (e.g. a simple series RL). But because this is such a generic point of view, people attributed other meanings to it, to cater to the various other use-cases. For example, a lowpass is better defines in terms of damping, \$\zeta\$, rather than the quality factor, because it provides a more intuitive description in the impulse or step response; a bandpass is better represented in terms of its center frequency, \$f_0\$, in relation to the bandwidth, \$\omega_{BW}\$ where time domain analysis is needed then it's also more descriptive to say that the higher the Q, the longer the settling time. All these make use of peculiarities of the application in order to provide a more intuitive description of the system or its response. How would all these sound if, for all the cases, there would be one explanation, only: the damping of the poles/zeroes. It would only hamper the understanding.
So, while the Q that you're talking about does, indeed, make sense only at one frequency, it doesn't mean that it's only the resonant frequency, or other, fixed frequency. It can be applied just about anywhere else, but a sensible choice would be where numerical analysis would give meaningful numbers (e.g. if \$f_0\$ = 1 MHz and Q is calculated at 1 Hz). And if that Q is used as the basis for series-parallel conversions, then that can only be done at one frequency, only, not necessarily at \$f_0\$.
Here is something to think about: use the same 2nd topology but calculate the parallel RL for a different frequency. This is one possible result, where the two circuits on the right have calculated values at 1 MHz and at 10 MHz: