Context
Veritasium - The Big Misconception About Electricity - Energy Doesn't Flow in Wires
Note I do not agree with the answer (D) given by Veritasium which is only plausible if any tiny current whatever is sufficient to "turn on" a source of light. However it may be the power coupling in the given geometry is sufficient to argue that a small source of light would "turn on" in a short interval of time after the switch closes.
Further Context
Online responses to the Veritasium video refer to the geometry either as a transmission line model or as an antenna model. I made a sketch of these alternatives as follows:
Applying right hand coordinates the y-axis points at the reader up out of the page. The z-axis extends toward the right of the sketch and the x-axis extends toward the top of the sketch.
I also made this sketch comparing (A) the text-book model of a transmission line with length in the z-direction; and (B) the approximate geometry of the Veritasium circuit:
The textbook transmission line model (A) does not apply directly to the Veritasium geometry; and the textbook model for a dipole antenna has a sine wave source and a length equal to 1/2 the wavelength of the source. So neither textbook model applies to the Veritasium geometry. I made sketch (B) as the first effort to comprehend how the geometry and properties of materials setup initial boundary conditions when the switch closes at \$t = 0\$.
This sketch of an equivalent system model (C), assumed to apply when the switch closes, represents my understanding of the answer by Andy aka:
Transmission Line Reference (Added Due to Answers Using TL Theory)
Transmission Lines (53 page pdf): https://my.ece.msstate.edu/faculty/donohoe/ece3313transmission_lines.pdf
See Page 5 (EM Wave Model Corresponds to Voltage-Current Model):
Comment: In my judgment the recognition of voltage and current associated with the transmission line contradict the assertion that "energy does not flow in wires". My recollection is that the material properties of the insulating medium impose a boundary condition on the surface of conductors where power develops and/or energy flows. This boundary condition may reduce the propagation speed along the conductor. The reduction of speed due to the boundary properties of the conductor and surroundings may be used to justify the statement that "energy does not flow in wires" but I think it is not completely accurate.
See Page 17:
In an answer below it appears to me that Andy aka applies this model where the source voltage \$V_g = 1 \$ volt step, this is physically adjacent to the bulb specified as the generator impedance \$Z_g = 100\$, and the end of the transmission line is a short circuit meaning \$Z_L = 0\$. Andy aka estimates \$Z_0 = 600\$ ohms characteristic impedance of the transmission line. There is no attempt to justify the use of this model in the context of the Veritasium geometry and it is not intuitively obvious to me why this model would apply.
Context of My Question
My question relates to the microscopic view of electric current in a lossless conductor and to the model for a long dipole antenna driven by a direct current step function. I would apply a model like this from Hyperphysics except using positive charge applying the positive charge carrier convention:
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/miccur.html
By ideal assumption the lossless conductor has infinite conductivity. This means energy will flow in or along the wire in perpetuity after all power sources and all power sinks are removed at some moment of time.
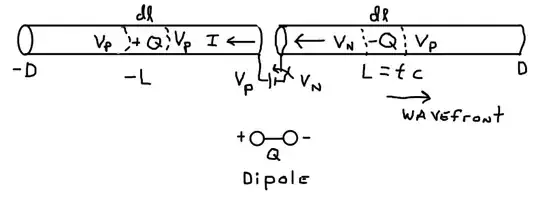
Below is a sketch of the lossless conductor coupled to the battery and switch. I want to understand and apply first principles for reasoning about the initial transient response in the lossless conductor just after the switch closes at time t = 0 {s}. Before the switch closes both sides of the lossless conductor have potential \$V = V_p\$ volt and current in the conductor \$I = 0\$ ampere.
I assume that when the switch closes at time t = 0 {s} the current steps up to a constant positive value, moving toward the left in the sketch, and the voltage wavefront develops on the right side of the conductor as shown in the sketch. The current has a magnitude \$I = V_p/Z_0\$ where \$Z_0\$ is the characteristic impedance based on the geometry and properties of materials in the stated problem. Note however I assume the current \$I = 0\$ on either side of the positions marked +L and -L. I do not know how to calculate \$Z_0\$ for the Veritasium geometry. Therefore I would rather begin the first principles analysis using the long conductor in isolation as shown in my sketch.
Assuming the wavefront moves with velocity \$v = c\$ {m/s} then the length \$L = tc\$ {m} and \$-L = -tc\$ {m} are functions of time. There is a potential difference \$V_p - V_N = V_B\$ moving with the wavefront at position +L where the battery voltage is \$V_B\$.
Note if there is an expanding dipole this means there is a net charge \$-Q\$ moving with the wavefront at \$+L\$ as shown in the sketch and a net charge \$+Q\$ moving with the current transition from \$I = V_P/Z_0\$ to \$I = 0\$ at the position \$-L\$. The length as a function of time is 2L = 2tc. This radiates an external electric field, outside the conductor, which is the field of an expanding capacitor.
If the length of conductor carrying current I is also increasing over time then this radiates an expanding magnetic field. The tendency of current to keep flowing in a long length of wire is associated with the model of an inductor. So the energy state of a capacitor and an inductor, both of length 2L, would be increasing with time provided my intuition about this model is confirmed by a properly reasoned analysis. Then any power coupling of the load (bulb) to this isolated system would reduce the power stored on the source side via negative feedback model.
Electrical power developed by the battery is \$P = IV_B\$ {W} at any moment of time. In an infinitely long lossless conductor the current flow at any instant of time would continue indefinitely if the battery is replaced rapidly by a short circuit. If the dipole model is accurate then there would be no further expansion of the dipole when power source is removed and then for lossless conductor the whole dipole configuration would move to the left with the flow of conventional current as a function of time.
Question
If there an external electric field caused by an expanding dipole region of total length = 2tc then how is this explained using the model for microscopic charge in a lossless conductor?