I am studying on a book (I'm still at basics) and I haven't understood why a signal with a lower number of harmonics implies a low bit rate. I have this figure:
It clearly shows how a signal with a high number of harmonics means that the bits are easier to "recognize". The bits in the last figure are 01100010. But it also shows the relationships between the number of harmonics and the bit rate:
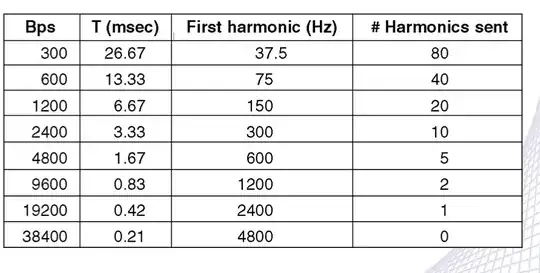
My question is: shouldn't it be the opposite? A signal with many harmonics could represent more bits than a signal with few harmonics. A signal with N harmonics is able to carry N bits in a certain period of time T, while a signal with just one harmonic can carry just 1 bit in T nano seconds. But there is something wrong in my argument, could someone clarify this?