Where is my capacitors energy missing?

Question

To avoid "mistakes", may I recall that, mathematically, \$\infty \times 0 \$ can be ... finite!

Otherwise, why use a Dirac impulse?

After reading this and this, I have yet a "question" about the energy stored in a capacitor and transferred to another capacitor of the same value to simplify "calculus".

Mathematical answer given by user150526 "May 22 '19 at 8:12".

But why is (s)he right ? Without any doubt. (When the wire is "resistive")

I have one capacitor C1, which value is 1uF, charged at voltage 100 V.

I have another capacitor C2 also of value 1uF which is discharged (V=0).

After wiring in parallel these capacitors, the common voltage is 50 V, no doubt.

While calculating the energy before wiring (C1), and after wiring (C1+C2), I find that the total energy is not the same. I have lost half of my energy which is "disappeared".

Where is this energy? Because energy can't be lost!

But how can I prove this, simply?

I "forget" the case if the wire can be considered as an inductor. So I made a simulation with a "theoretical" switch. And the transfer of energy can be done, almost with total efficiency.

Thanks also for a suggested proposal (from @bobflux) of superconducting wire between capacitors (wire as inductor). Very interesting as "superconducting wheel"?

Answer 1

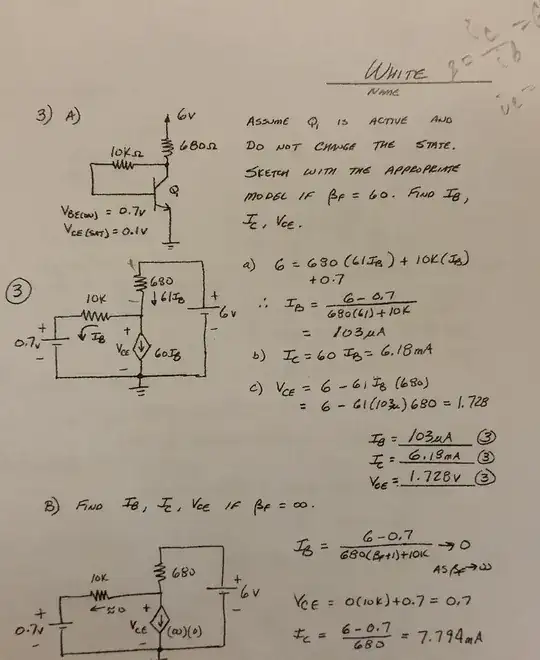
When you put the discharged capacitor in parallel with the charged capacitor, you get an immediate current flow of infinite amps and, that despite your observations about the Dirac impulse (which are not relevant), the infinite current is the root cause of your misunderstanding.

What can be said is: -

• Charge is conserved but,
• Energy is not necessarily conserved (without some care)

To conserve energy you need to avoid making a hard voltage connection to a capacitor. As an example of this, you are probably aware that the energy acquired by a capacitor is \$½\cdot CV^2\$ but, were you also aware that the total energy delivered from a hard voltage source into that same capacitor is \$CV^2\$ i.e. half the energy goes into the capacitor and half the energy is lost.

It doesn't matter how much or little series resistance you place between the hard voltage source and the capacitor, half the energy supplied is lost. Do the math or make a simulation, a large resistor will take longer to charge the capacitor but, will dissipate the same energy as a small value resistor. It doesn't take too much of a thought experiment to realize that this also applies when the resistance is zero ohms (impractical I know).

So, why do we use inductors as the intermediary energy storage device in boost converters - it's for that same reason; we can apply a fixed voltage source to an inductor and it will efficiently take energy from that voltage source then, when that inductor connects to the output capacitor, it also transfers that energy at 100% efficiency. This is because, to impart energy into a capacitor with high efficiency we need to charge it with current and not slap a big voltage across is instantaneously.

But how can I prove this, simply?

It's not that simple mathematically but, if you think of a voltage source that feeds a capacitor via a current regulating circuit, it's easy to demonstrate that the total energy entering the current regulating circuit is twice the energy available in the capacitor. Or, use a simulator and resistors.

To avoid "mistakes", may I recall that, mathematically, infinity∗0 can be ... finite!

This isn't applicable because the capacitor is still a hard voltage source at the moment of connection and therefore the "0" in your equation is actually indeterminate and certainly can't be regarded as zero.

Where is this energy? EDIT: Because energy can't be lost!

I'm sorry, but it can be "lost to the circuit". It turns to heat and that is not recoverable in a simple circuit.

---

A bit more on energy uptake and a mechanical analogy

Directly charging a capacitor from a voltage supply is inefficient. The energy consumed is C·V² but, the energy stored is only ½ C·V². Consider a 1μF capacitor charged to 1 volt and then connected to a discharged 1μF capacitor. Charge (C·V) is conserved hence, the final voltage is 0.5 volts. For energy there is loss: -

• Initial energy: ½ × 1μF × (1 volt)² = 500 nJ

• Final energy: ½ × 2μF × (0.5 volts)² = 250 nJ

The same happens when objects collide; momentum is conserved but energy is lost.

Inductors are different; all the energy taken from a supply is stored in the magnetic field. Unlike capacitors, inductors don’t cause a current surge. There’s no collision; current ramps up from zero amps in an orderly manner.

Energy is preserved.

Mechanical analogy: if an ideal motor winds up a spring then, all the energy consumed is liberated when the motor is reused as a generator. However, if a spinning motor were “applied” to a flywheel then, the energy acquired by the flywheel is only 50% of the energy taken/consumed by the motor.

There is a collision because the motor has to rapidly (and I mean rapidly) fall to zero rpm.

However, if a flywheel was progressively spun-up from rest then, energy transfer is 100%. Likewise, if a capacitor was charged by a ramping voltage, 100% transfer occurs. Inductors are useful; energy stored can be released into a capacitor with perfect efficiency. A charged inductor connected to a discharged capacitor will ramp the voltage from zero and transfer 100% of the energy to the capacitor.

Answer 2

The circuit has ideal wires (in fact, everything is ideal) so there is no resistance, and no inductance. Therefore, when the switch is closed...

If voltage on both caps is different, infinite current will flow from one capacitor to the other, that takes zero time, and after that, charge is equalized and half the energy has disappeared.

This is simply due to the model being too simple and unrealistic. It is like the collision of two rigid bodies. If they are infinitely rigid, then when they bump into each other, an infinite force will be involved during zero time.

If you want to solve it, I'd recommend adding a resistor of known value R in series with one of the wires, then solve the differential equations and calculate the energy state at t=0 and t=infinity. Notice it does not depend on the resistance, no matter how small it is, it will always burn half the energy. So asymptotically, even if the resistance is zero, it will still burn half the energy.

OK, let's use superconducting wires, then. No resistance, but there is inductance.

This one is realistic enough: it is an undamped LC tank, and when the switch is closed, it will resonate forever. Total energy in the circuit is constant, it just moves around between inductor and capacitor.

This circuit never reaches steady state, so you can't calculate the limit on this one with L going to zero to get back to the first circuit.

In a real circuit, energy would still decay due to the electromagnetic waves emitted by the circuit as AC current flows through it, and it would eventually reach steady state, with half the energy lost. Energy loss due to emitted waves is quite like adding a lossy element, for example a resistor, to the circuit.

Answer 3

Energy conservation is a real thing, idealised circuits are, well, idealised. When closing the circuit, the connecting wire will actually have resistance and inductivity. Even discounting the resistance, the inductivity produces a magnetic field that counteracts the current, leading to oscillation, and this oscillation with changing magnetic fields (inductance) and electric fields (capacitance) will radiate the energy that ends up missing when equilibrium is achieved.

Answer 4

Watch when you "wire"... Arcing!

Here is a simulation "proving" where this energy is lost (50%). It is obvious that the current grows as the resistor decrease. The waveforms remain relatively the "same", whatever resistance value.

Divide R by 10. Current increase x10 and time /10.

When current grows (if energy is enough), it is also obvious that the wire became very "hot" ... and then it melts, causing an arc in which half the transferred energy "dissipates" until it stop.

This is true regardless of the value of the resistance if "low". Ok, Resistance of arcing is not easy to simulate ... and is not very "constant".

So, the energy is not "lost" but became "heat".

But you can transfer energy without loss ... as this.