How can I solve this opamp circuit?

Question

I am designing an Analog Front-End circuit for an NTC Sensor which has 3 parts, the non inverting stage, the low pass filter, and goes to seeeduino.
Basically the input voltage is 5Vcc and I need to have a voltage output from 0 to 5V.
The NTC is the negative thermistor that changes according to temperature. R1 is there to act as a voltage divider that helps comparing the voltage entering the inverting side of the OA.

Both R1 and NTC are 10k ohm.
NTC is 10k at 25ºC (ambient temperature).
The opamp is an MCP6004.
The NTC range is: 27119 ohm at 5ºC, 10k for 25ºC and 4103 for 45ºC. I also have the Steinhart-Hart coefficients if necessary.

Answer 1

Your input is a voltage divider consisting of R1 and the NTC thermistor and fed with a 5V supply.
You've specified that for the 5ºC to 45ºC temperature range you're interested in, the resistance of your thermistor changes from 27.119k to 4.103k.
So, simple voltage-divider math tells us that the output from your voltage divider to the the opamp will be 1.35V to 3.55V - a range of 2.2V.

So the function you need from your opamp circuit is (approximately):
\$ Vo = 2.25(Vi - 1.35) \$
_{I've taken some liberties with rounding because resistor tolerances will introduce far more error than the rounding}

The 'ideal' circuit (if you had a fixed reference to use) would then simply be one with a gain of 2.25, using the reference to offset the value.
So the ratio of gain-setting resistors for a simple non-inverting configuration would be 1.25:1, since:
\$ Ao = 1 + (Rf / Ri) \$
      \$ = 1 + (1.25 / 1) \$
      \$ = 2.25 \$
and the reference you'd need would be:
\$ Vref = 1.35 + (\frac{1.35}{1.25k} \cdot\ 1k) \$
          \$ = 2.43V\$

So your resulting circuit might look something like:

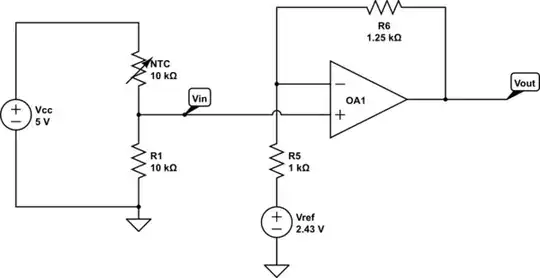
^{simulate this circuit – Schematic created using CircuitLab}

However you don't have a 2.43V reference - all you have is your 5V supply.
So what you can do instead is combine the 2.43V reference with the R5 resistor to produce an equivalent using your 5V supply and a fixed voltage divider.
To get 2.43V from 5V using a voltage divider you need a ratio of 1.056:1. And the parallel combination of resistors needs to be equal to 1k (or whatever value you end up choosing for R5).
For this 'ideal-ish' example, I'll choose resistor values of 1k94 and 2k06, which gives me 2.425V and 0.999k.
The circuit now looks like this:

^{simulate this circuit}

and produces roughly the same result as the previous version using the reference voltage.

However, these are not realistic resistor values.
To produce a more realistic circuit, I now start working backwards from where we are.
A pair of 'realistic' resistor values to use in a voltage divider which will give us about 2.43V from a 5V supply could be 5k1 and 4k7. This combination will actually give us about 2.4V.
That pair of resistors in parallel is about 2.45k - so the feedback resistor for the opamp needs to be 3k06 (2.45k x 1.25), so we'll choose 3k as a realistic value.
So now we have a circuit which looks like this:

^{simulate this circuit}

If you do the math or run the simulation, you'll find that this circuit now produces an output of approximately 0.06V to 4.95V for a temperature range of 5ºC to 45ºC.

Answer 2

This breaks down into the following parts, which you need to do, step by step:

1. Realize that your NTC + R1 form a voltage divider, which is connected to the non-inverting input of the opamp.
   1. Thanks to your info on the temperature range \$\Delta_T\$ you want to map to 0-5V, we can now calculate the resistance range the NTC will have.
   2. With that resistance range, we can calculate the voltage range at the non-inverting input of the opamp. Let's call that voltage rang \$\Delta_V\$.
2. You know that your output voltage range needs to be 5 V, but you only get \$\Delta_V\$ of range on the input, which is less than 5V. So, that defines the gain \$A\$ your opamp needs to have.
3. After applying the gain, the minimum voltage over the voltage divider \$V_\min\$ gets scaled to a voltage that's not 0V. So you need top subtract that offset, to shift your \$A\cdot V_\min\$ to 0 V. I.e., your offset \$B\$ needs to fulfill \$A\cdot V_\min+B = 0\$.

Now, the gain can be implemented simply by considering only the feedback resistor \$R_6\$, and a resistor to ground from the inverting input. If we imagine very hard that instead of \$R_3\$ and \$R_5\$, the non-inverting input, and \$R_6\$ & \$R_4\$, are directly connected to ground, we get the gain \$A=1+\frac{R_6}{R_4}\$. Nice! That's the first equation for our resistors; insert the \$A\$ you calculated from the voltage range relation above!

The offset \$B\$ can be achieved by not connecting to ground, but to a different voltage (the opamp simply doesn't care to which voltage it refers to). So, \$R_3\$ with \$R_4\$ gives us another voltage divider, which gives us a voltage that we can refer to as virtual ground.

Problem: This is a loaded voltage divider, so it won't work as good. This is only solvable by making the current flowing through the voltage divider in unloaded state (so, with \$R_5\$ imagined removed) much lager than any load current. Therefore, \$R_6, R_5 \gg R_3, R_4\$. But the simple voltage formula, which needs to generate \$B\$ from 5V, will then give us the second equation for our resistors.