Resistive divider as resistors approach 0 ohms

Question

Resistive divider when R1 = R2, split voltage in half because V = IR, and resistors in series add as Rtot = R1 + R2. It seems like this must break down as R1/2 approach 0 ohms. Anyone have a good explanation of the boundaries for when resistive divider behaves as the ideal in the equations? The wires can be assumed to be zero resistance, or, to be removed and just the resistors used for the circuit.

Answer 1

It is just a model. If you insist on assuming the wires have zero resistance, then making R1=R2 --> 0 always work, but the generator will have to source an ever increasing current (infinite current for R1=R2 -->0).

In the real world, the model breaks down when R1 and R2 approach the value of the actual wire resistance (several hundred milliohms or less, depending on the actual wire characteristics and material).

Anyway, in the real world you should also worry about the internal resistance of the generator and its current handling capability. If you lower R1 and R2 too much you will practically short the generator, with the ensuing smoke and even fire if it has no protection built in (e.g. an alkaline cell).

Answer 2

You may be charged ;) to learn that all batteries have an effective series resistance, ESR, that may be estimated by the V and mAh capacity.

• I use a 1hour current to estimate this source resistance.
• In solid-state supplies, they often give Load Regulation specs for current with some load reg. error ratio like 1% drop at some current. This also converts to an ESR value converting %V to actual.

Load Reg. Error: Vdrop/Irated=ESR.

Using any reasonable load can be used to test and calibrate this load regulation error and measure ESR from your "voltage divider relationship”.

An AA alkaline cell with 2500mAh with 1.5V for 10h has a ratio of 1.5V/ 2.5Ah = 0.6 Ohms.

However, due to Peukert's Law you can't consume 2.5Ah in 1 minute and the capacity drops rapidly, but all batteries are by design rated for 20h (hours) capacity drain current (A*20h) and is pretty close at 1h but drops appreciably below this. Charge rates also use C ratios that show how many times more than the 1h rate it can be used at , where this by design is dependent on both the electrical low ESR and low thermal resistance to remove heat.

When you assume an ideal battery, you are assuming your R divider total resistance is at least more than the tolerance errors you are allowing.

Answer 3

Anyone have a good explanation of the boundaries for when resistive divider behaves as the ideal in the equations?

Wires in the ideal world have zero resistance and no voltage drop, if a resistor has zero ohms it has no voltage drop and can be considered a wire. I will show this mathematically.

The voltage equation across a resistor looks like this:

$$ (V_1 - V_2)= I*R $$

so this is a better equation to use to find out what happens when resistance goes to zero (and since the divider equation can result from two of these equations)

$$ \lim_{R \to 0}(V_1 - V_2)= I*R \Longrightarrow(V_1 - V_2)= 0 \Longrightarrow V_1 = V_2 $$ There are two cases: the first one is if R1 goes to zero

$$ Vout = Vin(\frac{R2}{R1+R2}) $$

and you get

$$ Vout = Vin(\frac{R2}{R2}) \Longrightarrow Vout = Vin $$

which makes sense the circuit would look like this:

^{simulate this circuit – Schematic created using CircuitLab}

the second one is if R2 goes to zero

$$ Vout = Vin(\frac{0}{R1}) \Longrightarrow Vout = 0 $$

Which also makes sense because the circuit looks like this:

^{simulate this circuit}

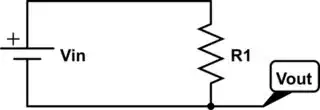
And we will measure zero voltage drop because we are measuring the voltage of the same point.