After explaining Ohm's law to someone who knew nothing about electronics, I was corrected by another guy, pointing out that not all components obey Ohm's law. I replied with the usual "I know, that's why I said in a simple resistive circuit."
However since I also know very little about electronics, that made me curious if that were really true. Is there any component for which the relation I = V/R is broken?
I always took that to just mean that this relation was constant, not that I could expect R to be constant and/or independent of the other two values or time. I wonder if, when people say that a diode (for instance) does not obey Ohm's law, do they actually just mean that you can't use it to set I by varying V or R independently?
Does a diode behave differently than a variable resistor which attempts to keep the voltage drop across it constant, and which offers maximum resistance when voltage across the terminals are reversed?
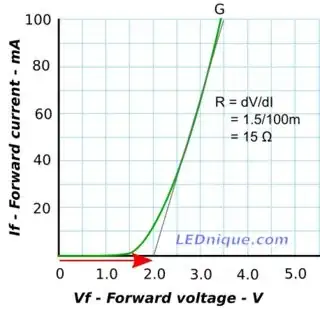
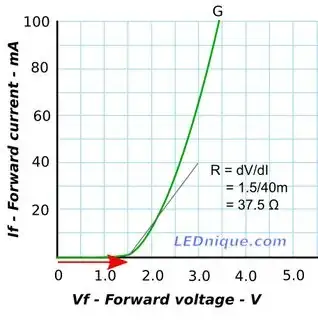
After reading the accepted answer here Does a diode really follow Ohm's Law?, I conclude that the answer to the last question is "no", that is, a diode does really "obey" Ohm's law. Can I also conclude that this is true for all components, if we use Ohm's original formulation, not later simplifications?
Does it even make sense to say that Ohm's law can be "broken"?