Common-collector Colpitts oscillator - feedback analysis

Question

I am a student working on a project where we are using CC Colpitts oscillators as local oscillators.

We've chosen the above values based on the condition g_m > w₀²C₁C₂R_L,series, which for the given image translates to g_m > w₀²C₁C₂R₆.

This is a formula we worked with as a given result (assuming biasing resistors are large in comparison to impedances at the resonant frequency), which I gather comes from the feedback network needing to have closed-loop gain > 1 and have the feedback signal be in phase with the input.

I wanted to arrive at this result myself but have been having some trouble. Here is how I have framed the problem and tried solving it:

1. The feedback topology is shunt-shunt, i.e. I am sampling the voltage at the emitter and then feeding a current back in at the base.
2. The feedback gain, B = j(1 / X_C1), since the feedback input comes into one end of C1 and the other end is grounded for feedback analysis (shunt connection).
3. Then for an open-loop gain A, the condition of A*B > 1 should allow me to solve for the previous result.

I then tried finding the loaded forward open-loop gain (A), loading the emitter with C1||C2 and the base with L||C1. However, here I got lost in the math and haven't been able to reduce A*B > 1 to the above result after multiple attempts.

I would appreciate any input of mistakes I may have made in the problem setup or help on how to proceed from here if the rest is right.

Answer 1

Consider the small signal model of the circuit (excluding the inductor) as shown below:

^{simulate this circuit – Schematic created using CircuitLab}

Here, I am assuming that, the operating frequency is much higher than the cutoff frequency of the bias circuit, \$\omega >> \frac{1}{C_3(R_7||R_8)}\$, which can be ignored. Also,I assume that \$\beta>>1\$ so that the base current can be neglected and \$\alpha = 1\$. The output resistance and the degeneration are assumed to be \$r_o, R_9 >> \frac{1}{g_m}\$ and are consequently ignored.
With these simplifications, KCL at node \$v_o\$ gives: $$(v_x-v_o)sC_1=v_osC_2+(v_o-v_x)g_m$$ $$v_o = \frac{(g_m+sC_1)v_x}{s(C_1+C_2)+g_m}$$ $$v_x-v_o = \frac{sC_2v_x}{s(C_1+C_2)+g_m}$$ KCL at node \$v_x\$ gives: $$i_x = sC_1(v_x-v_o)$$ $$i_x = sC_1.\frac{sC_2v_x}{s(C_1+C_2)+g_m}$$ $$\frac{v_x}{i_x} = \frac{C_1+C_2}{sC_1C_2}+\frac{g_m}{s^2C_1C_2}$$ $$Z_{eq}= \frac{1}{j\omega C_{eq}}-\frac{g_m}{\omega^2C_1C_2}, C_{eq} = \frac{C_1C_2}{C_1+C_2}$$ This is the impedance looking into the transistor which is a series combination of capacitance and negative resistance. The total impedance including the inductor becomes: $$Z_T = j\omega L+ R_6 + \frac{1}{j\omega C_{eq}} - \frac{g_m}{\omega^2C_1C_2}$$ For sustained oscillations, $$X_T = 0 \implies \omega L = \frac{1}{\omega C_{eq}} \implies \omega = \frac{1}{\sqrt{LC_{eq}}}$$ $$R_T < 0 \implies \frac{g_m}{\omega^2C_1C_2} > R_6$$ This gives the condition you mentioned in the question.

Answer 2

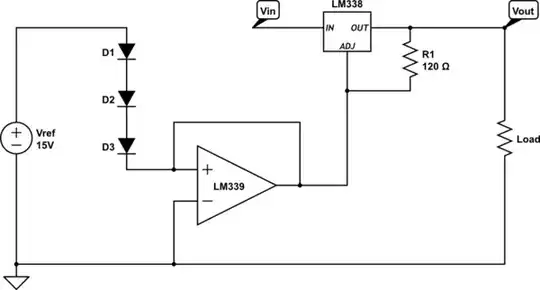
One can use 2 - port parameters as well. We will use the Barkhausen Criterion with current gains. It would seem natural to do this since the circuit is in common collector configuration. It is assumed that sinusoidal oscillation takes place. The Barkhausen Criterion in terms of current gain is:

$$A_i \beta_i = 1$$

The subscripts for the rest of this discussion;

$$ c \ \ and \ \ \beta $$

refer to the amplifier and feedback network parameters respectively.

We describe \$ \ \ A_i \ \ \$ and \$ \ \ \beta_i \ \ \$.

R. F. Shea writes that:

$$ \frac{I_2}{I_1} = \frac{y_{21}}{y_{11} + \Delta^y Z_l} $$

This is the current gain with \$ Z_l \$ as the output impedance. This was found and adapted from "Transistor Applications" by R.F. Shea (page 16). Thus:

$$A_i = \frac {y_{fc}}{y_{ic} + \Delta_c^y z_{in \ \ \beta}}$$

$$\beta_i = \frac{y_{21\beta}}{y_{11\beta} + \Delta^y_{\beta}z_{in \ \ c}}$$

\$ \ \ A_i \ \ \$ is the active device current gain. The current gain of a common collector configuration is negative. Assume \$ \ \ \Delta^y_c z_{in \ \ \beta} \ \ \$ is small where : $$ z_{in \ \ \beta} \approx r_{\epsilon} $$ Then: $$ \ \ A_i = \frac{y_{fc}}{y_{ic}} = h_{fc}. $$
where \$ \ \ y_{fc} \ \ \$ is the forward common-collector trans-admittance parameter and \$ \ \ y_{ic} \ \ \$ is the input admittance common-collector parameter. \$ \ \ h_{fc} \$ is a negative quantity. It is the common-collector "ac beta" of the transistor. Malvino writes that:

$$ h_{fc} = -(1 + h_{fe}) $$

This is equation (9-28) in "Electronic Principles" Paul Malvino third edition page 244. Now $$ \ \ \beta_i = \frac{y_{21\beta}}{y_{11\beta}} = -\frac{C_1}{C_1 + C_2 } \ \ (when \ \ \Delta^y_{\beta}=0) \ \ $$ This is the current gain of the feedback network or " the feedback fraction " of the oscillator . \$ \ \ y_{21\beta} \ \ \$ is the feedback network trans-admittance parameter and \$ \ \ y_{11\beta} \ \ \$ the feedback network input admittance parameter.
We note:

$$z_{in \ \ c} \approx h_{ic} $$

and is the output impedance of the amplifier. R.F. Shea writes:

$$ Z_i = \frac{1+ y_{22} Z_l}{y_{11} + \Delta^y Z_l}$$

where \$ Z_i \$ is the input impedance and \$ Z_l \$ is the output impedance.

This was also found and adapted from "Transistor Applications" by R.F. Shea page 16.

$$z_{in \ \ \beta} = \frac{1 + y_{22 \beta} h_{ic}} {y_{11\beta} + \Delta_{\beta}^{y} h_{ic}}$$

This is the input impedance of the feedback network with an output impedance of \$ h_{ic} \$. \$ h_{ic} \$ is in turn the input impedance to the common collector (emitter-follower) transistor amplifier.

The deltas \$ \ \ \Delta \ \ \$ are the determinants of the y matrices.

We now give a description of the feedback network.

$$ C_1 \ \ and \ \ C_2 $$ make up the usual split capacitor arrangement in a Colpitts Oscillator.
\$ \ \ C_2 \ \ \$ is connected to ground and \$ \ \ C_1 \ \$ is connected to the base of the BJT. The output impedance is taken from base to ground and terminated with \$ h_{ic} \$.
The junction of the two capacitors \$ C_1 \ \ and \ \ C_2 \$ goes to the emitter of the BJT and is the input to the feedback network. This is where the circuit between the junction of the split capacitors \$ C_1 \ \ and \ \ C_2 \$ and the emitter is broken. The inductance L is in parallel with \$ C_1 \ \ and \ \ C_2 \$. From this description the feedback network y parameters are expressed as:

$$ y_{11\beta} = j\omega(C_1 + C_2)$$ $$ y_{22\beta} = j\omega C_1 - j\frac{1}{\omega L}$$ $$ y_{21\beta} = -j\omega C_1 $$ $$ y_{12\beta} = -j\omega C_1 $$ $$ \Delta^y_{\beta} = -\omega^2 C_1 C_2 + \frac{C_1 + C_2}{L}$$

Let \$\Delta_{c}^{y} z_{out\beta} \approx 0 \$

From the Barkhausen Criterion: \$ \ \ \ \ \ \ \ \ A_i \beta_i = 1 \$ \$ \ \ \$

$$ \frac{h_{fc} \ y_{21\beta}}{y_{11\beta} + \Delta_{\beta}^{y} h_{ic}} = 1 $$ This is found by multiplying \$ A_i \ \ and \ \ \beta_i \$ and equating with 1 which implies Equation 1:

$$ h_{fc} y_{21\beta} = y_{11\beta} + \Delta_{\beta}^{y} h_{ic}$$

We divide both sides by \$ \ \ y_{21\beta} \$.

$$ h_{fc} = \frac{y_{11\beta}}{y_{21\beta}} + \frac{\Delta_{\beta}^{y} h_{ic}}{y_{21\beta}}$$

The real and imaginary parts must be separated and equated and we arrive at the real part corresponding from equation 1: This is equation 1a (the condition for oscillation):

$$ h_{fc} = \frac{y_{11\beta}}{y_{21\beta}}$$

$$ \omega \neq 0 $$

From the imaginary part of equation 1 we obtain equation 1b (the frequency of oscillation):

$$ \frac{\Delta_{\beta}^y h_{ic}}{y_{21\beta}} = 0 $$

We now analyze equations 1a and 1b:

From equation 1a: $$h_{fc} = -\frac{C_1 + C_2}{C_1}$$

$$-h_{fc} = \frac{C_1 + C_2}{C_1}$$

\$ -h_{fc} \$ is a positive quantity.

From equation 1b (or the imaginary part) :

$$ \Delta_{\beta}^y \ = 0 $$

the frequency of oscillation is obtained:

$$frequency = \frac{1}{2\pi \sqrt{L C_{eq}}}$$ where

$$C_{eq} = \frac{C_1 C_2}{C_1 + C_2}$$

Maybe this might help.