I'm trying to smooth out the steps from a digitally-generated LFO signal which changes step-wise. The digital steps are small, but still audible when the LFO is hooked up to the circuit that uses it (zipper noise).
I'm considering using a low-pass RC filter. I'd like to predict the effect it would have so I can decide if it will be a useful approach. Are there any free or affordable resources I could use? I'm pretty much a layperson when it comes to electronics, so the simpler the better.
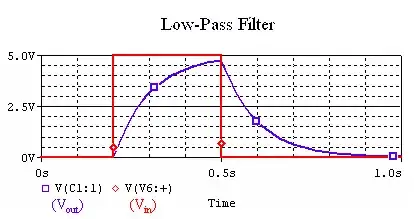
Given that the effect of a low pass RC filter on a square wave is asymptotic, something like this (borrowed from here)...
... my assumption about how an RC filter works is that the gradient of the filtered signal is proportional to the voltage differential between the filtered signal and the source signal; and that the proportionality is determined by the R and C values.
Edit I've TL;DR;ed the question - the accepted answer says everything I was trying to elicit.