V=IZg
V=IaZ
IaZ=IZg
LdIc/dt+RIc=(L+Lg)di/dt+(R+Rg)i
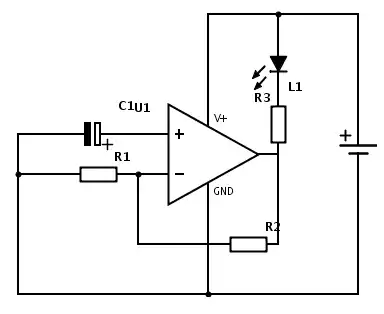
simulate this circuit – Schematic created using CircuitLab
Hi ,
how can I get state space model in the form of dx/dt=Ax+Bu?
Ic is input and I is the state variable. I am getting derivative of Ic as input. How can I eliminate that?