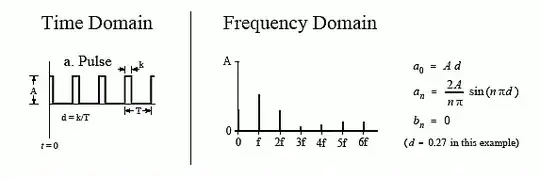
After reading this question I was wondering about another scenario where the signal is not a square wave but a pulse train with short ON time.
As far as I understand, if we have a 3 MHz pulse train signal with 50% duty cycle which is coupled by a 50Ohm coax cable to a scope, we can consider that the 7th harmonic of 3 MHz (21 MHz) is the highest frequency we need to be interested in maintaining. That has a wavelength of 14.28m. So if we exceed this length we need to use 50Ohm termination at scope input.
But how about if we have 3MHz pulse train with 2% duty cycle(ON time 6.6ns ), will the above logic apply to roughly determine the critical length to use 50Ohm termination?