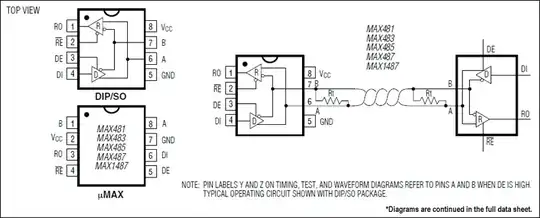
The first figure shows the layout of a metal wire and current flowing in the metal from left to right.
Assume that that the sheet resistance of the metal is Rs (Ω/sq) then the resistance of the square 3W x 3W with such current flowing is just same as Rs, the sheet resistance of the metal.
Now consider the case where there is a zero-ohm contanct in the center of the square. The current flows from left side to the square and entering the contact from all directions and then though the contact to the bottom layer.
So I'm trying to calculate the resistance of the blue part if current flowing in all directions to the contact as shown in the image.
The result is 0.65*Rs but I would like to know if there is a general approach to prove this. I heard that it can be done by using integral but I haven't figured out how to do that.