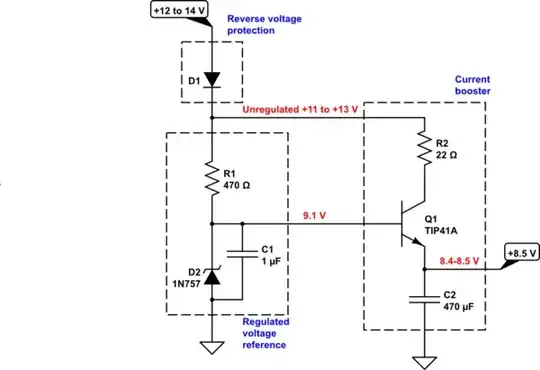
Considering a negative feedback system, the closed-loop transfer function Af is given by:
where A is the open-loop transfer function and AB is the loop gain.
Every text I read says that if the magnitude of the loop gain is much larger than one, then the closed-loop gain becomes:
whereas if the loop gain is much smaller than one, the closed-loop gain becomes equal to the open-loop gain A.
I would perfectly agree with these approximations if all the quantities were real. But in general both the open-loop gain as well as the loop gain are complex quantities.
Question: how can I prove that if the magnitude of the loop gain is much larger than one, then the closed-loop transfer function is approximately equal to 1/B? Here my calculations:
In the last expression, I cannot go on: I would like to get rid of the term 2Re(BA), so that the square root would become exactly the magnitude of the loop gain and would simplify with the numerator.