The H4n is a great device, if pricey (but not overly priced.)
Balanced and unbalanced/single-ended
I guess the first thing to discuss is the meaning of balanced and unbalanced, since it's more a technical issue between experts and has far less real meaning to consumers. Between experts, as I've interpreted what I have read (as I'm no expert here, just a hobbyist trying to follow along at times), it appears that balanced means differentially amplified.
Many phantom-powered, XLR microphones (not all by any means) are balanced in exactly this sense. Figure 1(c) in an answer by Transistor provides an example of what I mean here.
Unbalanced is often taken as synonymous with single-ended. That would be like Figure 1(a) in the above link.
Microphones are transducers. Speakers are transducers. These are devices that convert between dynamic electronic signals and some dynamic physical property of interest. Since humans don't directly perceive (well) electronic signals directly, transducers are what make an electronic device useful to us.
Transducers can be operated in balanced mode and they can be operated single-ended, or unbalanced. In addition to the balanced XLR microphone design just mentioned, there are bridged amplifier outputs to drive speakers and these may also be considered as balanced outputs. Amplifier outputs can also be unbalanced -- that's quite commonly the case, in fact.
In between the input transducers and the output transducers, amplifier systems may have intermediate stages. And once again, these stages can also be balanced (differential) or unbalanced (single-ended.)
That's my hobbyist perceptions of what I've read from experts (Burkhard Vogel, for example.)
[Since I speak German as a 2nd language I can't help add that Der Vogel is "the bird" while Die Vögel is the plural form, as in "the birds."]
The point to the above is not to get too "hung-up" on the idea of balanced inputs and outputs. It's a specialist term used between specialists to discuss differential vs single-ended propagation of signalling. (There are noise and other technical reasons for caring, and/or paying for balanced signalling.)
The term does not necessarily also mean that the output impedance equals the input impedance, though that may be the case at times for technical reasons.
When should the impedance be matched?
When the specifications say they should be.
Or when you are wanting to deliver the maximum power into an output transducer or get the maximum power from an input transducer. There is a maximum power theorem that says that the maximum power is transferred when the output impedance matches the input impedance.
A low impedance output to a high impedance input works to get most of the signal voltage across, one to the other.That's the goal. This is neither a balanced/unbalanced question nor an impedance-matching question. It's just a matter that most amplifier systems operate with voltage-signalling and you want to get the maximum signal across, one to the other. Not the maximum power (except again in those rare cases where that's important.)
You still have to meet specifications, though. There are reasons not to have extremely high impedances involved, for example. (Noise is one such reason.) There are reasons where you want extremely high impedance. (A voltmeter is one such reason.)
So, read the specs and make sure that you are within range of what they can handle. If your input source tells you that it cannot drive a \$480\:\text{k}\Omega\$ input, then your H4n unbalanced input doesn't meet the specs and probably won't work as well as it should. But it's unlikely that you will have a microphone source that works poorly with such a high impedance input. Still, it's possible. I think the H4n designers figured that anyone using an unbalanced input isn't focused explicitly on noise issues as the most important factor, or else they wouldn't be using unbalanced inputs. So they focused instead on presenting as light a load as possible in order to have the least possible impact on the input source, despite noise considerations of doing so.
Just use the H4n and be happy. ;)
Maximum power theorem
Well, you said you wanted mathematics. :) Tip me over with a feather, will you?
Suppose you have a source of power which has an intrinsic source voltage and source impedance and you want to extract the maximum possible power. You have the freedom to choose the load impedance. So you want to know, "What's the optimal impedance to use, in this case?"
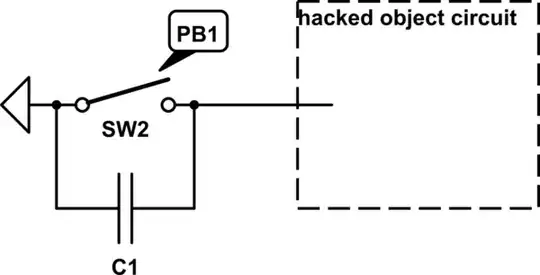
simulate this circuit – Schematic created using CircuitLab
$$\begin{align*}
I_{_\text{TOTAL}} &= \frac{V_{_\text{SRC}}}{R_{_\text{SRC}}+R_{_\text{LOAD}}}
\\\\
P_{_\text{LOAD}} &= I_{_\text{TOTAL}}^2\cdot R_{_\text{LOAD}}
\\\\
&=\left[\frac{V_{_\text{SRC}}}{R_{_\text{SRC}}+R_{_\text{LOAD}}}\right]^2\cdot R_{_\text{LOAD}}\tag{1}\label{1}
\end{align*}$$
You want to maximize Eq. \$\ref{1}\$. This is done by taking its derivative (slope equation) with respect to \$R_{_\text{LOAD}}\$ and solving for the case where that slope becomes zero. (Where the slope is zero is either a maximum or a minimum.)
The derivative is:
$$\begin{align*}
\text{D}\bigg[P_{_\text{LOAD}}\bigg] &=\text{D}\left[\left(\frac{V_{_\text{SRC}}}{R_{_\text{SRC}}+R_{_\text{LOAD}}}\right)^2\cdot R_{_\text{LOAD}}\right]
\\\\
\text{d}\,P_{_\text{LOAD}} &= \left(\frac{V_{_\text{SRC}}}{R_{_\text{SRC}}+R_{_\text{LOAD}}}\right)^2 \left(\frac{R_{_\text{SRC}}-R_{_\text{LOAD}}}{R_{_\text{SRC}}+R_{_\text{LOAD}}}\right)\text{d}\,R_{_\text{LOAD}}
\\\\
&\therefore
\\\\
\frac{\text{d}\,P_{_\text{LOAD}}}{\text{d} R_{_\text{LOAD}}} &= \left(\frac{V_{_\text{SRC}}}{R_{_\text{SRC}}+R_{_\text{LOAD}}}\right)^2 \left(\frac{R_{_\text{SRC}}-R_{_\text{LOAD}}}{R_{_\text{SRC}}+R_{_\text{LOAD}}}\right)
\end{align*}$$
Setting that to zero, we know that the first factor can't be zero so we can focus on making the second factor equal to zero, instead. The numerator there makes this obvious:
$$\begin{align*}
R_{_\text{LOAD}}&= R_{_\text{SRC}}
\end{align*}$$
So, there's the maximum power theorem.
When does maximum power transfer matter?
One of the few times where any consideration of maximum power may be wanted is with headphones where their impedance can vary widely. These typically today vary from \$8\:\Omega\$ to \$600\:\Omega\$. (Only one manufacturer actually makes the same model in such a wide range, though.) Some older ones, difficult to acquire today, were designed for crystal radios when they were far more popular. The better quality ones may present typically somewhere between \$2\:\text{k}\Omega\$ and \$4\:\text{k}\Omega\$.
Higher-impedance headphones use very thin wire, on the order of 20 microns in diameter, offering a lower movement mass. Because the wires also leave less air between windings, the voice-coil's magnetic field is stronger. When a manufacturer takes good advantage of these benefits, the result is a more sensitive and better sounding product with lower distortion.
Suppose a cellphone designed to accept a \$32\:\Omega\$ headphone load that provides, at most, \$2\:\text{mW}\$ (maximum volume setting.) Assuming the cellphone's output impedance is very low by comparison, and it will be quite close to zero given the usual feedback factors involved, this implies \$V_{_\text{RMS}}\approx 250\:\text{mV}\$.
But what about jacking in a professional headphone, rated at \$600\:\Omega\$ impedance? That same cellphone would now only deliver \$100\:\mu\text{W}\$.
A \$32\:\Omega:600\:\Omega\$ audio transformer would match the impedance. The ideal turns-ratio would be about 1:4.33 -- computed as \$1:\sqrt{\frac{600\:\Omega}{32\:\Omega}}\$. Then the same \$600\:\Omega\$ headphone would be reflected over to the cellphone and presented as the expected \$32\:\Omega\$ load. (Add the transformer to the headphone first and then plug the resulting pair into the cellphone.)
Ignoring insertion losses for now, the RMS voltage appearing at the headphone is now \$V_{_\text{RMS}}\approx 1.1\:\text{V}\$ and delivers, you guessed it \$2\:\text{mW}\$, into the headphone load. (A real audio transformer will have insertion losses. But not uncommonly near \$1\:\text{dB}\$.)
More on this topic can be found in "Ch. 15: Audio Transformers" from Glen Ballou's 5th edition of "Handbook for Sound Engineers," 2015. See, in particular, the discussions concerning Figure 15-24:
So that may be reason to match impedance. But this is an uncommon circumstance where the intent is to maximize power delivered into a transducer. For most audio hook-up arrangements, this isn't the goal.



