I'm having trouble understand what's going on in this circuit. The question asks "what is the value of Q if \$\bar{R} = 1\$ and \$\bar{S} = 0\$" (as shown).
In this case, how can I determine what Q looks like? I realize that this question may require knowledge from the one above, which is why I asked it first. Any information about where to go would be great.
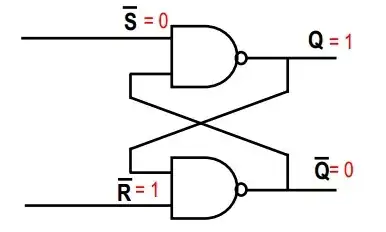
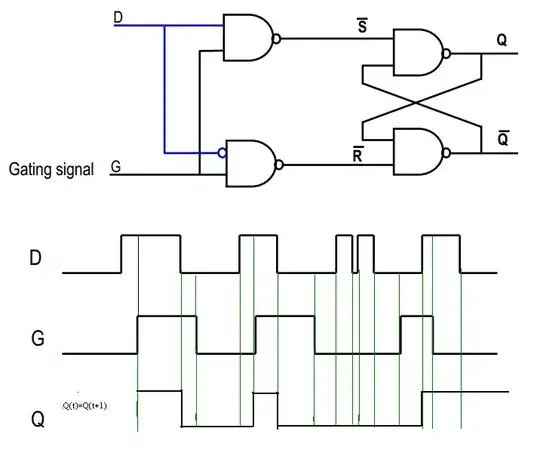
In your first picture, consider the top NAND gate. We know that a NAND gate is such that, if any input is 0, then the output must be 1 (the only way the output of a NAND gate is 0, is if both inputs are 1). Thus, since ~S = 0, then Q = 1, regardless of the second input to the top NAND gate.
Since you now know both inputs to the second NAND gate, it is easy to deduce that ~Q = 0 (both inputs are 1, so the output of the NAND gate is 0)
~S = 0
~R = 1
Q = 1
~Q = 0
The point of the circuit is that, if you now set ~S = 1, the outputs will not change, because the second input to the top NAND gate is 0 from before (both inputs must be high to make the NAND output change to 0). So now you have:
~S = 1
~R = 1
Q = 1
~Q = 0
Consider this: What if your initial conditions were switched, i.e. ~R = 0 and ~S = 1? Doing the exact same reasoning as before (except that we now begin with the bottom NAND gate) we find that Q = 0, and ~Q = 1
~S = 1
~R = 0
Q = 0
~Q = 1
Now the magic happens: we set ~R = 1. What happens? It might help to draw it out, but basically, the outputs will not change due to the same argument we had before; the other input to the NAND gate is already 0, and we need both inputs to be 1 in order to change the output (~Q) to 0. (There is a hint that this would happen, since the circuit is perfectly symmetrical)
~S = 1
~R = 1
Q = 0
~Q = 1
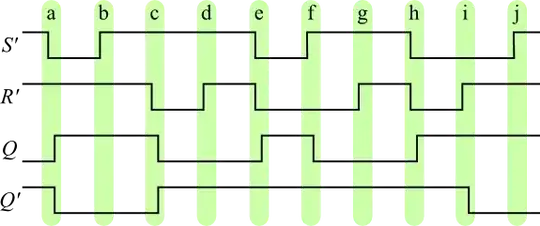
The inputs are the same as before, but the outputs are different! - they remember the previous state.
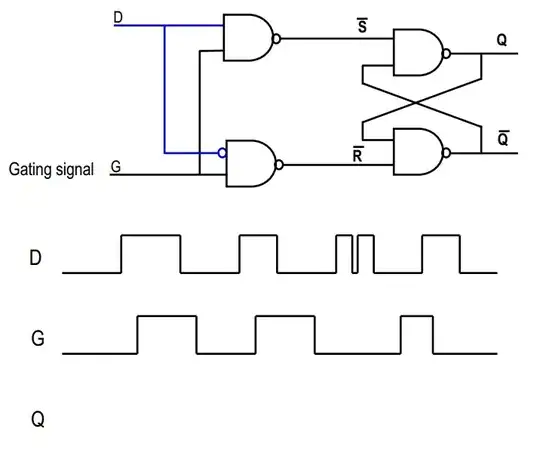
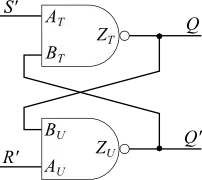
In general, you will never use the case when both ~S = 0 and ~R = 0, because then both Q = 1 and ~Q = 1, which will probably break the logic that is depending on the circuit. That is the point of the two extra gates in your second picture; they protect the SR flip flop so that this particular input will never happen.
(Think of S as "set" and R as "reset" - when both are low, the flip flop remembers the previous state. When S is high, you "set" the output (Q) to 1; when R is high, you "(re-)set" the output to 0. If you try to set the output to 0 and 1 simultaneously, something wrong will obviously happen, so you need to make sure it doesn't happen.)
In your second picture, consider the "D" signal: It goes straight into first NAND gate, and an inverted version goes into the second. Now, if D is high, then the second NAND will always output 1, so that ~R = 1. On the other hand, if D is low, then the output of the first NAND will always be 1, so that ~S = 1. In this way, we guarantee that our frightening scenario with the SR flip flop above will never happen, yes?
Now consider the G signal. If G = 0, then both ~S = 1 and ~R = 1; thus, this is the "remembering" state, in which the output stays the same. However, if G = 1 then either ~S or ~R will be low, right? Which will depend on the value of D.
In short, when G is 1, then Q = D, and when G is 0, then Q = Qold
The first circuit is a standard "flip-flop" or "latch". Here is a truth table:- $$\array{\bar{S}&\bar{R}&Q&\bar{Q}\\0&0&1&1\\1&0&0&1\\0&1&1&0\\1&1&?&?}$$ The interesting thing is that last row, with \$\bar{S}=\bar{R}=1\$ there are two stable states for the output, \$Q=0,\bar{Q}=1\$ and \$Q=1,\bar{Q}=0\$. This means that it can essentially "remember" which of the inputs \$\bar{S}\$ and \$\bar{R}\$ was last seen at \$0\$.
Now let us look at the first half of the second circuit. $$\array{D&G&\bar{S}&\bar{R}\\0&0&1&1\\1&0&1&1\\0&1&1&0\\1&1&0&1}$$ While \$G=0\$ it outputs \$\bar{S}=\bar{R}=1\$ and so the flip-flop remains unchanged in whichever stable state it last held. But when \$G=1\$ the value of \$D\$ will set the state of the flip-flop, and by combining both tables we can see it sets \$Q=D\$.
I agree with the OP in that the critical part of the function of a D-latch lies in it's SR-latch, so I will focus on that part only for the moment.
Since we're dealing with NANDs here, I would derive the SR-latch function or truth table from that of a NAND with the inputs A and B and the output Z:
$$ \array{A&B&Z\\0&0&1\\0&1&1\\1&0&1\\1&1&0} $$
Looking at your SR-latch schematic, naming the upper NAND (driven by S') "T" and the lower NAND (driven by R') "U", we have the following relationships:
$$ A_T=\bar{S}, B_T=\bar{Q}, A_U=\bar{R}, B_U=Q $$
From that, we can start to draw a truth table for the SR-latch, from which we know only the inputs at this point:
$$ \array{A_T=\bar{S}&&A_U=\bar{R}&&B_U=Q=Z_T&&B_T=\bar{Q}=Z_U\\ 0&&0&&&&\\0&&1&&&&\\1&&0&&&&\\1&&1&&&&} $$
Looking back at the truth table for the NAND, we realise that if any of it's inputs A or B is 0, it's output Z is 1. From that, we can start to fill in the missing values in our SR-latch truth table:
$$ \array{A_T=\bar{S}&&A_U=\bar{R}&&B_U=Q=Z_T&&B_T=\bar{Q}=Z_U\\ 0&&0&&1&&1\\0&&1&&1&&\\1&&0&&&&1\\1&&1&&&&} $$
Now, looking at the NAND truth table again and realising that it's output Z is 0 if both A and B are 1, we continue filling in the missing values:
$$ \array{A_T=\bar{S}&&A_U=\bar{R}&&B_U=Q=Z_T&&B_T=\bar{Q}=Z_U\\ 0&&0&&1&&1\\0&&1&&1&&0\\1&&0&&0&&1\\1&&1&&&&} $$
Seems like we have got all entries except the one for when both S' and R' are 1, because this state is only dependent on the previous Q and Q' values. This is how the latch holds its value, because for that state, the NANDs' inputs look like
$$ \array{A_T=\bar{S}=1, B_T=\bar{Q}\\A_U=\bar{R}=1, B_U=Q} $$
from which follows that the outputs of these latches are
$$ \array{Z_T=!\bar{Q}=Q\\Z_U=!Q=\bar{Q}} $$
Labelling these "previous" Q and Q' values as Qp and Qp', we have the final truth table for our SR-latch:
$$ \array{A_T=\bar{S}&&A_U=\bar{R}&&B_U=Q=Z_T&&B_T=\bar{Q}=Z_U\\ 0&&0&&1&&1\\0&&1&&1&&0\\1&&0&&0&&1\\1&&1&&Q_p&&\bar{Q_p}} $$
If you prefer to look at some waveforms of this SR-latch built from NAND gates, the following might help:
The values for Q and Q' in this diagram can be derived from looking at the truth table of the SR latch:
To the OP: If that is not clear or you'd like some more details (such as more schematics of the different states), please let me know in a comment - I'll see what I can do.
nand-gate is determined will be 1 if one of its input is 0.
so Q would be 1 and pass this 1 into down side nand-gate.
then noth two nand-gate's inputs are 1 so Q-bar is 0
you can check if Q-bar affects any input.
The important thing to realize is that in CMOS logic, the output is always defined and driven to zero or one, anything in between is a transient state. Set the two outputs (Q and Q') to any of the four "possible" states, step time forward discretely and propagate the ones and zeroes through the system and see where things settle. Remember that a NAND gate presented with a zero on one of its inputs always outputs a one, and a NAND gate presented with a one on one of its inputs acts like an inverter applied to the other input.
When ever S bar and Q bar are 1. then the present Q did not change i mean Q(t)= Q(t+1). When S(bar)=0 then Q=1 and when R(bar)=0 then Q= 0
