Why does Andy aka's calculation work in this case?

Question

This question is from a confusion from this thread.

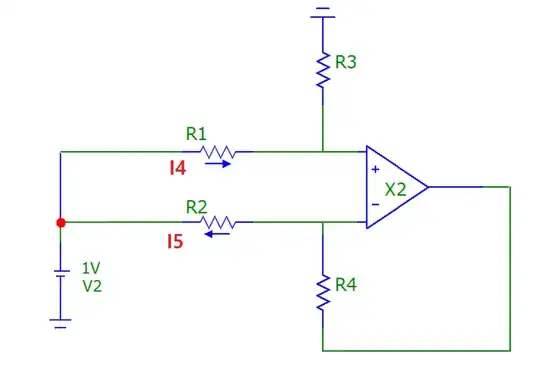
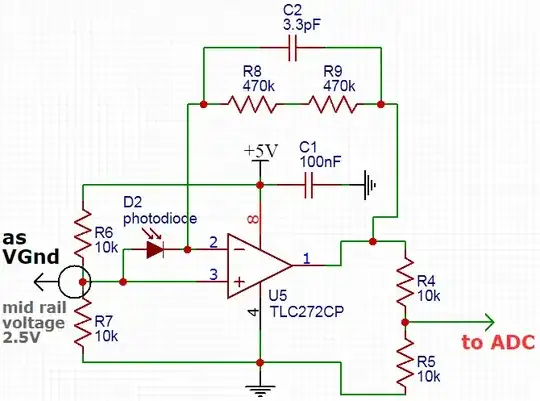
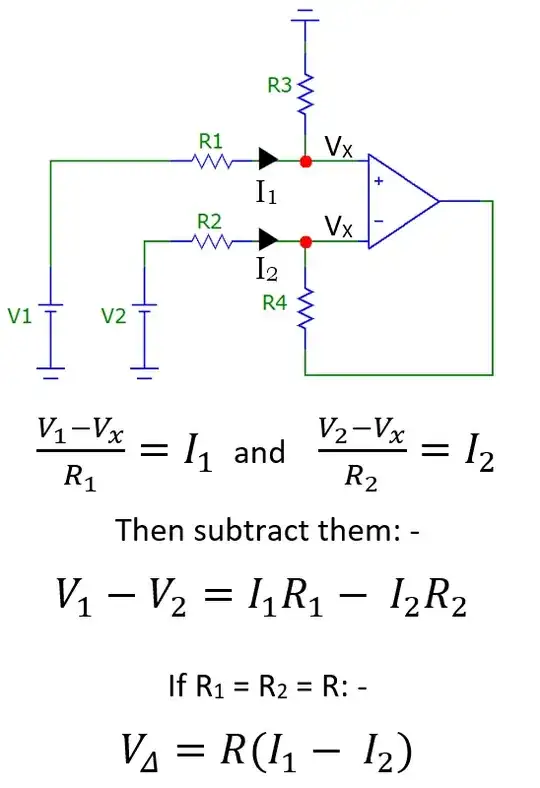
Assume that you have the opamp circuit shown below. Also assume that the opamp is ideal and you don't know the value of R1, R2, R3, R4.

Now you do two measurements:

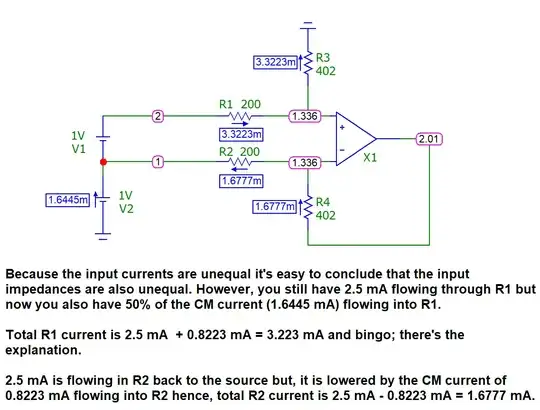
1. Apply a voltage 1V between Vp and Vn and you measure the current I1 = I2 = 2.5mA as in the image.

2. Apply differential voltage V1 = 1V and common mode voltage V2 = 1V as in the image below. You cannot measure the currents I4 and I5 directly. The only current you can measure is I3. Now you look at the ampere meter and see I3 = 1.6445mA.

Question:

Can you calculate the value of I4 and I5 from the two measurements above?

In this post Andy aka calculated it like this:

I4 = I1 + I3/2
I5 = I2 - I3/2

This gives the correct results in that case, but what is the theory behind it?

COMMENT:

What Andy did looks a bit like superposition but actually it is not.

With superposition you would do it as follows:

First you set V1 = 0 and calculate I4, I5.

Next you set V2 = 0 and calculate I4, I5.

Now you notice that the circuit is different from Andy aka's circuit in the first case above as the node Vnis now grounded.

The current through R1, R2 is now not 25mA anymore.

Finally sum I4, I5 from two cases above to get I4, I5 caused by the two voltage sources.

Note that I'm not asking how to calculate voltages and currents at any nodes and branches like what Jan did. I can easily do that using circuit analysis techniques like nodal, mesh analysis, etc.

It seems like everyone misunderstood my question. I'll express it again in the image below.

Answer 1

A mistake in your question states that 25 mA is flowing; it's 2.5 mA not 25 mA.

Consider this first image (now your 2nd image due to you editing your post): -

This circuit has no forcing CM voltage applied. You see that 2.5 mA flows into R1 and 2.5 mA returns through R2. Because the op-amp creates a virtual-earth, both inputs to the op-amp can be regarded as being at the same potential. For DC considerations this is a very exact approximation and, only op-amp offset voltages and offset currents might make this slightly untrue.

So, given that the currents are the same magnitude (2.5 mA) AND that the op-amp inputs take zero current ideally, we can say, with high-confidence that R1 = R2.

We can also say that the loading impedance on the differential source (V1) is 400 Ω. I don't think this needs explaining given that 1 volt results in 2.5 mA flowing through R1 and R2. And, given that R1 = R2 we then know that R1 = R2 = 200 Ω.

Now, when you push that 1 volt source up a little bit with a forcing CM voltage as per your 2nd (now your 3rd) diagram, extra currents flow from left to right into both R1 and R2 but, the differential currents (the 2.5 mA from above) still remain but, are added to or partially cancelled by the extra currents from the forcing CM voltage.

Your basic question is why the two extra currents flowing left to right through R1 and R2 are equal. Clearly those extra currents add up to 1.6445 mA (your 2nd picture) but, why should an extra 0.82225 mA flow into R1 and why should an extra 0.82225 mA flow into R2.

Firstly, if 0.82225 mA flows into R1 then the impedance seen by the 2 volts at that node has to match 2 volts with 2.5 mA + 0.82225 mA i.e. there has to be an impedance of 602 Ω. And that tells you what R3 is i.e. 402 Ω (because R1 is 200 Ω. And, because this circuit is a balanced differential amplifier we know that R4 must also be 402 Ω.

So, now we have all the resistor values. But we cannot say from the outset what you said: -

Also assume that the opamp is ideal and you don't know the value of R1, R2, R3, R4.

We cannot say that completely because that would not represent a balanced differential amplifier (reference my original post that you are concerned with). And, my original post made that absolutely clear. So, a better thing to say is R1 = R2 and R3 = R4. We must say that because it's a balanced differential amplifier.

I showed this picture in my original post: -

And, given that the differential input voltage will continue to force 2.5 mA into R1 and take 2.5 mA from R2, it's simple math to see that the two extra currents are equal.

---

This should be sufficient to demonstrate that the difference in current into the two input resistors is completely due to the difference in voltage applied to the two input terminals: -

It follows from this that the op-amp output voltage is proportional to the differential input voltage when R1 = R2 and R3 = R4.

Answer 2

Here is my method of analysis of this circuit with a floating V1 source at the input.

From this diagram, we can see that \$V_P = I_{IN}R_3 = V_N\$ (due to negative feedback action).

Additional we see that \$V_1 = I_{IN}(R_1 + R_3)\$ and \$V_2 = V_N - I_{IN}R_2 =I_{IN}R_3-I_{IN}R_2 \$

Therefore:

$$V_1 - V_2 =I_{IN}R_1 + I_{IN}R_3 -I_{IN}R_3 + I_{IN}R_2 = I_{IN}(R_1 + R_2)$$ $$I_{IN} = \frac{V_1 - V_2}{R_1 + R_2}$$

Knowing this we can solve for the output voltage

$$V_{OUT} = V_N + I_{IN}R_4 = I_{IN}(R_3 +R_4) =\frac{V_1 - V_2}{R_1 + R_2} \times (R_3 +R_4) = (V_1 - V_2) \frac{R_3 + R_4}{R_1 + R_2} $$

And the gain is:

$$ \frac{V_{OUT}}{V_1 - V_2} = \frac{R_3 + R_4}{R_1 + R_2}$$

But due to the fact that we want CM gain to be equal to \$A_{CM} = 0\$ we need to meet this condition \$\frac{R_4}{R_1} = \frac{R_3}{R_2}\$. Thus, \$R_4 = R_3\$ and \$R_1 = R_2\$. So we can simplified the gain expression to:

$$ \frac{V_{OUT}}{V_1 - V_2} = \frac{R_4}{R_2}$$

Now if we add a CM source to the circuit we have this new situation.

And because we have a linear circuit we can try to apply the superposition principle. To find \$I_3\$.

$$I_3 = I_4 + I_5 = 2 \times \frac{E_2}{R_1 + R_3}$$

We assume \$A_{CM} = 0\$ and \$R_4 = R_3\$, \$R_1 = R_2\$

$$I_4 = \frac{I_3}{2}$$ $$I_5 = \frac{I_3}{2}$$

And finally

$$I_{R1} = I_1 + I_4 = I_1 + \frac{I_3}{2} $$

$$I_{R2} = I_2 - I_5 = I_2 -\frac{I_3}{2} $$

Answer 3

This answer is only for the problem with the superposition to calculate the currents.

Superposition for two voltages is typically done with the cases \$(V1=0, V2)\$ and \$(V1, V2=0)\$.

But that is not necessary.

It can also start from any known \$(V1, V2)\$ with the cases \$(V1 + \Delta V1, V2)\$ and \$(V1, V2 + \Delta V2)\$. This follows clearly from the linearity of the circuit.

E.g. \$ I1 = A*(V1 + \Delta V1) + B*(V2 + \Delta V2) \$

There is surely a book with a proof.

Assume R1=R2. I1 flows to the right. I2 flows to the left. Vx is the voltage on the Opamp inputs.

We start with the differential circuit. That is without the CM voltage source V2 (really removed).

Like all have shown

$$I1 = I2 = \frac{V1}{(2*R1)}$$

Now calculate the voltage at the bottom of \$V1\$. I call it \$V1n\$.

$$ V1n = I1*(R1+R3) - V1 = \frac{V1}{2*R1} * (R1+R3) - V1 = V1*\frac{R3-R1}{2*R1} $$

Set the value of \$V2\$ to \$V1n\$ and connect it to the circuit. The two circuts are equivalent, because the voltages and the currents are the same. Through \$V2\$ flows no current.

Now increase \$V2\$ by \$ \Delta V2 \$ to its final value. Here it is \$ \Delta V2 = 1V - V2 \$.

This is the superposition but only with a change of \$ \Delta V2 \$. The calculation can be done only with the \$ \Delta's \$ in the circuit.

$$ \Delta I1 = \frac{\Delta V2}{R1+R3} $$

$$ \Delta Vx = \Delta I1 * R3 $$

$$ \Delta I2 = \frac{\Delta Vx - \Delta V2}{R2} $$

Alltogether gives

$$ \Delta I1 = - \Delta I2 $$

The rest follows.

Hope there is no big error.

Answer 4

• Superposition will always apply if the 2 critical specs are met, namely; Vcm input and Vout are both within the linear range
• Vdiff to the OP Amp is always 0V and Vcm only rises to some ratio of the V2 = applied.
• The Idiff currents I1, I2 remain the same and reject the common mode current applied as you expect from CMRR.
• Thus you expect the new Idiff currents (I1,I2) to be raised by the Icm (I3) applied
• although the Voltage across R1,R2 is always equal they are not necessarily equal current magnitudes (given that all R values are unknown)
• !
• the single ended currents have changed by Vcm being added, and the resistors values are unknown, you cannot assume they are split equally by 1/2. Thus the new I1,I2 are unknown. The other answers are fallacious because by example they assumed equal R’s.

The bottom line is that the output voltage now has an error if the resistors pairs (R1=R2, R3=R4) are NOT equal, when any common mode voltage is applied (AC or DC).

Even though the differential current remained constant any tolerance errors in this match affect the CMRR and results in a conversion to an error in the output voltage to compensate for the change in single ended source currents with negative feedback.

——

If we assume a balanced R ratio for diff gain and balanced sum for each leg for CM rejection, we can explain this without math.

Since R1 & R2 are terminated with a null difference voltage, the current loop is always constant as long as the linearity conditions are met. The added current from Vcm=1V will see the Thevenin Equivalent resistant of both equal branches (R1+R3=R2+R4) in parallel so V2 must supply twice the added current or in other words each branch splits the V2 input current equally.

Answer 5

Nota : the two circuits are "different" ... so superposition can't be applied, even if results can be correlated.

Theoritical assumptions ... All Rx are equal. OPamp : Uplus = Uminus

First case : U1 = 1 ; IR1= U1/(2R1) ; IR2 = U1/(2R2) ;

Second case :

U1 = 1 ; U2=1 ; Up = (U1+U2) ; Uplus= Up / 2 = 1V ; I3 = I'R1= (U1+U2) / (2*R1) = 2 *IR1 ;

As inputs of OPamp are at same level ... I5 = I'R2=0 ;

So I(U2) = I3 = 2 * IR1

-> I5 =I'R1= I3 /2 + IR1 ; I4 = I'R2 = I3 / 2 - IR1 = 0 ;

Unless I made a sign error ...

If R3 = k * R1 ; R4 = k * R2 ... and I4-(-I5) = constant= 2 * I1.

The resistance of ammeter is not taken into account !

In fact, it is more simpler ...

case 1 : I1 = I2 -> I1 - I2 = 0 but I1 - (-I2) = 2 * I1 (always)

So (node between U1 and U2) (eq 1) I4 = I3 + I5 and (eq 2) I4 - (-I5) = 2 * I1 (constant)

Solving (1) and (2) give :

adding (1) and (2) -> 2 * I4 = I3 + 2 * I1 -> I4 = I3 / 2 + I1

substracting -> I5 = - I3 / 2 + I1

For request of someone ...

Adding Math sheet picture : Maple software

In picture I forget ... adding_currents ... # C = i1 + i2 := 2 * i1 ... which is constant !!!

Adding Microcap circuit picture for Dynamics DC Analysis

Answer 6

In general, I4 or I5 varies upon R4, R2, R3, and R1. Thus, with given information, I4 & I5 are not deterministic.

a) In the circuit of "1.", we can close the circuit at the OPA input node, Vcm. Since I1 & I2 includes all the current;
I1 = I2 = (Vp-Vn) / (R1 + R2).This resolves in:
(R1 + R2) * (2.5mA) = 1V ---(1)

b) In the circuit "2.",
I3 + I5 = I4, I3 = I4 - I5, Thus,
I4 - I5 = 1.6445mA ---(2)

c) Meantime,for the same sense as "a)",
V1 = I4 * R1 + I5 * R2 = 1V ---(3)

While solving for I4 & I5, along with two other variables (R1 & R2), I could not come up with another set of equation (too lazy :-).

However, the solution exists when the resistor sets are consisting a differential amp with balanced impedance,
R1 = R2 ---(4)

---

Question 1: "Can you calculate the value of I4 and I5 from the two measurements above?":
Answer: 'No', for general solution, 'Yes', with another condition provides an unique and proper equation. That another condition was "differential amp with balanced impedance", then;

I1 = I2 = 1 / (R1 + R2) --- (1)
I3 + I5 = I4 --- (2)
I4 * R1 + I5 * R2 = 1V ---(3)
R1 = R2 ---(4); "differential amp with balanced impedance"

Question 2: "Andy aka calculated it like this: I4 = I1 + I3/2, I5 = I2 - I3/2"
Answer: As explained, "differential amp with balanced impedance" was assumed to come up with that equation.
When R1 == R2 (balanced impedance), from eq(1),
R1 = R2 = 2 x I1 = 2 x I2 --- (1.1)

Substituting eq(1.1) to eq(3),
I4 + I5 = 1/(2 x I1) = 1/(2 x I2) ---(3.1)

Rewriting eq(2),
I4 - I5 = I3 ---(2.1)

eq(3.1) + eq(2.1) => I4 = I1 + I3/2 ---(Andy's 1)
eq(3.1) - eq(2.1) => I5 = I2 - I3/2 ---(Andy's 2)