Differentiator and integrator - without op-amp

Question

I am trying to understand the working and function of the integrator and differentiator circuits using op-amps.

Can someone tell me why we need to use op-amps for that function? Selecting just the right value of RC components (appropriate time constant values) according to our input signal would also perform the same function, right?

What advantage does the op-amp give us and what disadvantage does the usage of RC circuits for the differentiation and integration functions gives us?

"Selecting just the right value of RC components (appropriate time constant values) according to our input signal would also perform the same function, right?" No, you have to use opamp. — Marko Buršič, Jun 17 '21 at 07:56
I suggest that you use a circuit simulator like LTSpice and build these circuits with and without opamps. Then compare their behavior. Which ones have in a more "ideal" behavior? For example, generate a square-wave signal and use an integrator to convert that into a triangle-shaped wave. — Bimpelrekkie, Jun 17 '21 at 07:58
@Newbie, I want to ask you honestly: Do you need even simpler and clearer explanations, which, however, require some reaction on your part? I ask you because I have noted that your questions are interesting and they provoke such answers... but once you get them, you does not react... Why? — Circuit fantasist, Jun 17 '21 at 18:28
@Circuitfantasist, I am not sure what you mean by that I do not react? — , Jun 18 '21 at 04:29
@Newbie, If you asked an interesting question, it stimulates the participants to answer it with an (even more) interesting and original answer. It would be good for you to rate this not only with "+1" but also with an (albeit short) comment where you can show what you understood and what you did not understand. You can also ask an additional question. Thus, a small discussion can take place, as a result of which the issue will be fully clarified. — Circuit fantasist, Jun 18 '21 at 18:01

danmcb · Accepted Answer · 2021-06-17T15:08:02.813

10

You don't need the opamp, in theory. A simple, passive, RC circuit gives you am integrator or differentiator (otherwise known as first order low pass/high pass filter).

One problem is output impedance and loading. The opamp allows you to create a similar circuit which has very low output impedance, and whose characteristic will not be significantly altered when connected to a real world load, in the order of kilohms to megohms.

Input impedance might also be an issue if the output impedance of the driving signal is not very low. This could also be solved by using an opamp buffer.

A second problem with a passive integrator is that it has an exponential response to a constant input, whereas an opamp integrtaor has a linear one (until it reaches its limit of course).

edited Jun 17 '21 at 15:08

answered Jun 17 '21 at 07:58

danmcb

6,009
14
29

4

The main problem of the RC integrating circuit is its nonlinear (exponential) curve through time when a constant input voltage is applied. – Circuit fantasist Jun 17 '21 at 13:50
1

you are correct! updated. – danmcb Jun 17 '21 at 15:02
In principle, the same applies to an active integrator as well. However, this effect is hardly to identify because of the very large MILLER capacitance. So - it is common practice to neglect this effect. – LvW Jun 17 '21 at 15:50
@LvW, Here is an illustration of my "meta" comment that I just wrote under Spehro's response a while ago. The op-amp integrator is something qualitatively different from the ordinary RC integrating circuit; its curve is thousands of times more linear than the exponential curve of the RC circuit... so we can consider it as a straight line. Talking about circuit imperfections at the stage of understanding kills the understanding of the fundamental idea. This is a basic principle in inventive (creative) thinking. – Circuit fantasist Jun 17 '21 at 19:57
Different people have different principles for explaining physical phenomena - no surprise there. Therefore, I cannot agree with your last sentence. There is no fundamental difference in the operation of the simple RC element and the active MILLER integrator. In both cases the output voltage is the time integral over the current flowing through the resistor. The only difference is that the time constant of the active circuit can be very large. I think that this knowledge is the basis for understanding both circuits. – LvW Jun 18 '21 at 06:28
@LvW, There is a significant difference between the passive RC integrating circuit and the active op-amp inverting integrator. This difference is not only quantitative, it is qualitative. In the former, the voltage drop across the capacitor is subtracted from the input voltage; as a result, the current gradually decreases and the voltage slows down. In the latter, the op-amp copies the voltage drop across the capacior and adds it to the input voltage. As a result, the "current-creating" voltage and accordingly the current, stays constant so the voltage across the capacitor linearly changes. – Circuit fantasist Jun 18 '21 at 18:23
Sorry, but I disagree. The difference is quantitative only. Let me explain: Under realistic conditions (real opamps), also in this case, the current through the resistor is determined by the difference Vin-Vn (Vn: Finite voltage at the inverting opamp terminal). Hence, we have the same principle as for the passive RC case (causing disturbed integration). That means: The difference between both cases is quantitative (but this effect is much smaller in the opamp case). – LvW Jun 18 '21 at 19:03
...continued: As the result of this non-ideality, the phase response exhibits a 90 deg phase shift at one single frequency only (it is very hard to see this effect in the magnitude response). It is a well-known fact that the phase response reacts much more sensible to non-idealities than the magnitude of a function. – LvW Jun 18 '21 at 19:05
@LvW, I did not expect that professors from technical universities with long experience would have to argue in what order circuits should be explained since it is clear to everyone that this has to be done from the simple to the complex... and that the simple is ideal (idealized), and the complex is real... Simple here means to apply a constant input voltage and to think of the op-amp as an amplifier (proportional device) ... and in this way to reveal the fundamental idea behind the circuit. OK, ask what OP has found out from your last comment above; the answer will be "nothing". – Circuit fantasist Jun 19 '21 at 10:21
My last comment (both parts) are a reply to your statement (that the "difference" between both circuits would be not "quantitive" but "qualitative"). Hence, it was not an answer to the OP. On the other hand, when my explanations are not wrong, some newbies could gain some additional insights into the relation between time and frequency domain for integrating circuits - and this could be something more than "nothing". I repeat: In both circuits, the capacitor C is charged by a current I=(Vin-Vx)/R with Vx=Vc (passive) resp Vx=Vn (active). A pure quantitative difference. – LvW Jun 19 '21 at 12:31
@LvW, No, the difference is qualitative... and there are a few qualitative differences. In the op-amp version: 1) the input resistance is constant = R; 2) the input current is constant = VIN/R; 3) the output resistance is zero; 4) the output voltage VOUT has the opposite polarity of VIN; 5) the graph is linear. However, the question arises what is "qualitative" and what "quantitative" for you. I think we need to set some threshold and so we get two "qualities"... but we usually do it intuitively... E.g., we say the RC circuit is *bad* (imperfect) and the op-amp circuit is *good* (perfect)... – Circuit fantasist Jun 19 '21 at 13:48
OK, the discreapency can be solved quickly: Two circuts: (a) Passive R=1.6k and C=1milliF grounded) ; (b) R=1.6k and C=1µF (not grounded) but paralleled with an inverting amplifier with A=-999. The second circuit (b) has exactly the same transfer function as the the first one (a) - when the output is taken at the inverting amplifier input. In both cases, the charging current for C is determined by the voltage across the resistor (equal in both cases). When you say that both circuits will work fundamentally (qualitative) different , we have a different understanding of the term "qualitative". – LvW Jun 19 '21 at 15:07
I forgot to mention that the second circuit provides - as you know - a second low-resistive output (amplified and phase shifted by 180deg). This is the main advantage of the active circuit; more than that, the capacitor value is allowed to be much smaller. I consider this difference as a quantitative one. – LvW Jun 19 '21 at 15:12
Let us [continue this discussion in chat](https://chat.stackexchange.com/rooms/126667/discussion-between-circuit-fantasist-and-lvw). – Circuit fantasist Jun 19 '21 at 16:55
OK - I have answered... – LvW Jun 20 '21 at 12:54
An RC low pass filter only forms a reasonable integrator for time scales much less than the RC time constant. Otherwise the errors become quite large. – user4574 Jun 21 '21 at 16:00

score 5 · Answer 2 · edited Dec 26 '21 at 20:06

5

Consider the simplest possible input to the integrator (a constant voltage) and compare the behavior of the two circuits.

schematic

^{simulate this circuit – Schematic created using CircuitLab}

(I've added an inverter to the op-amp integrator to give an output that is the positive integral of the input voltage, for easy comparison).

We know ideally the integrator will output a straight line ramp starting at the initial voltage and increasing at 1 V/100 ms.

From the simulation we can see that the op-amp circuit does that, however the RC circuit does not. Initially it starts off with the same slope, however as the output voltage starts to approach an appreciable fraction of the input voltage (1 V in this case) the divergence increases. It will never even quite get to 1 V, whereas the op-amp output will increase until the op-amp itself runs into some kind of limit (such as getting too close to the positive rail for the op-amp to work properly).

The op-amp integrator also has a low output impedance, which is a useful secondary effect. In this case, the op-amp input "looks" like a 100 kΩ resistor to (virtual) ground, whereas the RC circuit is not as simple.

If it is a current that you are integrating, a capacitor alone will do that perfectly, however an op-amp integrator circuit (think of the above circuit with R1 = 0\$\Omega\$ and V1 replaced with a current source) has the input as a virtual ground. That's a great advantage in some situations (for example, if the current source is a photodiode) since it almost eliminates the voltage change across the PD, greatly increasing the circuit performance because the PD capacitance has little effect on the circuit speed.

edited Dec 26 '21 at 20:06

Elliot Alderson

31,192
5
29
67

answered Jun 17 '21 at 13:42

Spehro Pefhany

376,485
21
320
842

*"From the simulation we can see that the op-amp circuit does that, however the RC circuit does not."* And how does the op-amp circuit do this magic? – Circuit fantasist Jun 17 '21 at 15:44
@Circuitfantasist We could spend a lot of electrons or a few describing that. A simple way (and doubtless rather unsatisfying to you) is that the op-amp acts as a voltage-to-current converter so the capacitor 'sees' a current that is proportional to the input voltage and unrelated to the output voltage. – Spehro Pefhany Jun 17 '21 at 15:47
There is no "magic" at all. A real opamp increases the effective capacitance due to the MILLER effect. Hence, the response of the real circuit is - of course - not a "straight line", however, we cannot see the difference and we treat the opamp as "ideal". However, its non-ideality can be seen very easily: The ac response shows that the phase shift will be not ideal (90 deg), the phase response crosses the 90 deg line at one single frequency only. – LvW Jun 17 '21 at 15:57
@Spehro Pefhany, I see... but the role of the op-amp is a key point in understanding the circuit and should be revealed and well explained... Well, *"the op-amp acts as a voltage-to-current converter"*... but how does this "magic" work so the humble resistor acts as an "ideal" voltage-to-current converter? – Circuit fantasist Jun 17 '21 at 16:52
@LvW, Let me remind you that unexplained more sophisticated circuit phenomena (such as virtual ground, bootstrapping, dynamic load, etc.) can be explained by simpler (even non-electrical) phenomena. The Miller effect does not belong to the latter because it itself needs a simpler explanation... – Circuit fantasist Jun 17 '21 at 17:03
@LvW, I would also add that circuitry is not a religion to follow literally any canons. It is not necessary to have everything explained somewhere as you, as a rule, try to present in your comments denying the new and original circuit explanations. On the contrary, they should be encouraged... – Circuit fantasist Jun 17 '21 at 17:11
1

@Circuitfantasist That magic is referred to in my answer with respect to the virtual ground, so the op-amp becomes an almost ideal voltage to current converter. Sounds like you're itching to write an answer, so please have at it. We already have answers that approach from the frequency domain and the time domain and your unique approach can't hurt. – Spehro Pefhany Jun 17 '21 at 17:14
@Spehro Pefhany, You said it very figuratively (apparently this idiom is used in all languages). I got this "itching":) in the early 90's when I was able to first explain this circuit and then summarize my explanation and apply it to all op-amp inverting circuits. I have told this story in the [talk page](https://en.wikibooks.org/wiki/Talk:Circuit_Idea/Voltage_Compensation) of the Wikibooks story of [Voltage Compensation](https://en.wikibooks.org/wiki/Circuit_Idea/Voltage_Compensation). I have shared my explanation here a few times. I would do it now if OP wants it but I am not sure... – Circuit fantasist Jun 17 '21 at 17:54
Circuit fantasist - I really cannot see where I have tried in my "comments denying the new and original circuit explanations." I have some problems to understand the background of your comment. May I ask you to clarify ? – LvW Jun 17 '21 at 18:07
@LvW, Well, if Spehro lets us, I will say a few "meta" words here. I am not against your approach, I just note that we are opposites. I am an inventor at heart and always look for original explanations of circuit phenomena; I do the same with my students... I teach them to think and understand, not just to memorize. I do the same here and I encourage and do not discourage others from doing so. If we all do that here, SE EE will be a much better place than it is now. Just a personal opinion... – Circuit fantasist Jun 17 '21 at 19:32
1

@Circuit fantasist, when you read my single comment above again you will notice that I did nothing else than to mention the fact that the non-idealities of the opamp integrator can best be seen by inspecting the phase response. So - I dont know which "approach" you are referring to. I cannot see where I have "discouraged others"..... – LvW Jun 18 '21 at 06:41
@LvW, We know each other very well in forums and there is no need to explain in detail. But still, sometimes I am surprised and I want to ask you, "Do you really think that such a basic question should be answered in scientific terms like "phase shift", "phase response", etc.?" But this is an extremely simple concept that can be seen all around us in all its manifestations... and everyone knows what it is about... You don't have to have studied the whole control theory to understand it... – Circuit fantasist Jun 18 '21 at 07:28
@Circuit fantasist, the basic question was "What advantage does the op-amp give us and what disadvantage does the usage of RC circuits for the differentiation and integration functions gives us?". Dont you think that the answer to such a question should mention the phase shift (which you call "scientific term")? Dont you think that the phase shift of an integrator is a fundamental property of the circuit which should be part of an answer to the question? How can you say that - by mentioning the phase shift - I will "discourage others" ? With all respect, I cannot understand.... – LvW Jun 18 '21 at 07:38
@LvW, Only to note that, for the purposes of revealing the fundamental circuit idea, it is not necessary to introduce frequency and phase terms because it is sufficient to consider the case of DC input voltage. – Circuit fantasist Jun 18 '21 at 18:46
Sorry, but I must disagree. The integrator function is characterized not only by the timely magnitude response but also by the phase shift between input and output (ideally 90 deg). This is one of the two criteria which are exploited for realizing filter functions. – LvW Jun 18 '21 at 19:10
1

@Circuitfantasist - the basic principle by which the op amp improves the linearity of the RC basic circuit, is: gain is cheap. The RC basic circuit works well when RC is large; the op amp version works well when A* RC is large, A being the op amp voltage gain. – Whit3rd Jun 20 '21 at 20:41
1

@Whit3rd, Agree... but only to add that you will never imagine how the op-amp inverting amplifier operates if you think of the op-amp as of a high speed amplifier. You have to think of it as of a slow acting servo... or human being (like the student in 2001)... – Circuit fantasist Jun 20 '21 at 21:27
@Spehro Pefhany, I think I managed to scratch my "itch" very well - :) – Circuit fantasist Jun 21 '21 at 06:30
@Circuitfantasist I like your idea of the manual op-amp, along similar lines to H&H’s “Transistor Man” – Spehro Pefhany Jun 21 '21 at 06:33
Exactly, @Spehro... Last night I was hesitant to call it "Op-amp man"... true... Just to add that the setup in front of the students is a kind of data acquisition system that displays on the monitor the "course" of the capacitor voltage over time - "exponential" (if the student stops moving the potentiometer viper) and *linear* (he moves it so that there is a zero voltage on the voltmeter connected between the RC middle point and ground)... It was very attractive... I think I have a movie from a similar "conceptual experiment" with the *Deboo integrator* (I sent it then to the very Deboo)... – Circuit fantasist Jun 21 '21 at 06:44

LvW · Answer 3 · 2021-06-17T18:45:38.980

4

Yes - a simple RC circuit can be used (theoretically !) as an integrator - under the assumption that the time constant T=RC is very large. For example:, with R=100k and C=10µF the pole frequency is wp=1 rad/s and the range of intergation will approximately start for w>100 rad/s.

What does the opamp? It not only allows to connect a load (without influence to the integration process) but it will drastically increase the effective capacitance by a factor which is identical to the (very large) open-loop gain of the opamp. This is due to the well-known MILLER effect. Therefore, such an intergator is called "MILLER integrator".

MILLER effect (in short):

When a capacitor C is connected between the input and the INVERTING output of an amplifier, the current through C is much larger (due to the amplified and inverted output voltage) if compared with the current driven from the input voltage only. Hence, the effective conductance wC seems to be much larger (if seen from the input only and when compared with the product wC for the selected value of the capacitor).

Example: C=1nF connected between input and (inverting output).

Current through C without an amplifier: i1=V_in*wC
Current through C (between v_in and v_out=-A * v_in): i2=[v_in-(-A*v_in)]*wC.
Comparison: i2/i1=(1+A).
For case 2, the current through C is larger by a factor of (1+A); that means: The capacitor C acts as if it were larger by the factor (1+A).
Note that for an opamp we have A=A_open loop.

edited Jun 17 '21 at 18:45

answered Jun 17 '21 at 08:56

LvW

24,857
2
23
52

Thank you for your answer. But, I have not got the concept of Miller effect understood. Any simple explanation you can provide to understand the Miller effect in basic terms? – Jun 17 '21 at 10:22
Please, see my edit (MILLER effect) – LvW Jun 17 '21 at 10:55
Why are you putting Miller in all caps? – Hearth Jun 17 '21 at 13:46
2

Sorry, but I could not get your message. What do you mean with "all caps"? I spoke only about one single cap between input and inverting output! – LvW Jun 17 '21 at 15:45
"caps" = "capital letters" – Circuit fantasist Jun 17 '21 at 20:43
@LvW Why are you typing it as "MILLER" instead of "Miller"? "all caps" means "all capital letters". – Hearth Jun 17 '21 at 22:15
Thank you for this clarification. You are asking "why"? I am afraid I cannot give an answer, perhaps just a "habit"? – LvW Jun 18 '21 at 06:34

score 3 · Answer 4 · answered Jun 17 '21 at 14:03

3

There are already given several answers of RC integrators and RC differentiators and how they in certain conditions do something which resembles integration or differentiation.

But a capacitor alone does both of them and it does them very well. That's because capacitors obey the following law:

Charging current = Capacitance x The growth rate of the voltage.

That could be reversed by saying that the capacitor integrates the charging current.

So, is it integrator or is it differentiator depends on which quantity (current or voltage) is the input and which is the output.

This, of course, causes some difficulties if one wants both input and output as voltages. Operational amplifier is a good help for this. The common opamp based integrator converts the input voltage to charging current and the common opamp based differentiator converts the charging current to voltage.

answered Jun 17 '21 at 14:03

Very good answer with some ingenious guesses... Ah, if only you could clarify your last sentence, an excellent answer would be... – Circuit fantasist Jun 17 '21 at 15:33
OK. I'll add a clarification later. – Jun 17 '21 at 15:58
user287001, is it really the "common opamp based integrator" which converts the input voltage into a charging current? I don`t think so. The integrator does nothing else than to integrate the voltage. Rather, it is just the resistance R between the signal input and the inverting terminal of the opamp (which is nearly at ground potential) who does this conversion. This does not work for a simple passive RC circuit because the current through the resistor is not determined by the input voltage only! – LvW Jun 17 '21 at 16:05
It charges the capacitor between -input and output of the opamp. The -input stays at GND potential, - the opamp sets Uout such way - The input current is Uin/R and that charges the capacitor because opamp inputs do not take substantial current when compared to other currents in a well designed circuit. Converting the input voltage to charging current is the mechanism how the common integrator does that "nothing else, but integrates" – Jun 17 '21 at 16:11
Yes - thats exactly what I was saying: It is the resistor R (and not the whole integrator circuit) which provides the charging current i=v_in/R. – LvW Jun 17 '21 at 16:14
A similar consideration applies to the diff. circuit: It is the resistor R which converts the current i=C(dV_in/dt) into the output voltage. – LvW Jun 17 '21 at 16:19
about "not the whole integrator": I'm afraid it stops working in the same way if some of the parts is removed - opamp, resistor, capacitor or a wire. – Jun 17 '21 at 16:43
@LvW, The resistor R only provides the charging current i = v_R/R since it "sees" only the voltage drop v_R across itself. It does not "know" that v_R = v_in - v_C + v_out = v_in - v_C + v_C = v_in - 0 = v_in and, as a result, i=v_in/R... The op-amp supplements v_in with v_C and, in this way, it creates the illusion that the input voltage is applied across R. – Circuit fantasist Jun 19 '21 at 10:38

Circuit fantasist · Answer 5 · 2021-12-26T18:17:57.013

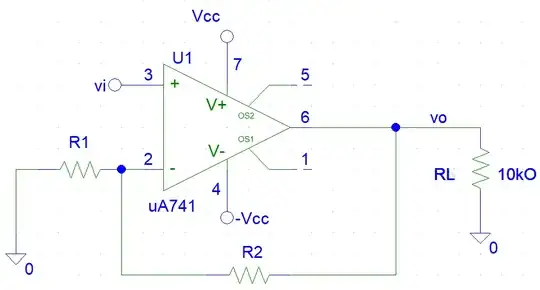
Can someone tell me why we need to use op-amps for that function?

Short answers

Here are two short but comprehensive answers - in the first, the op-amp is considered attached to the input voltage source; in the second, it is considered attached to the capacitor:

The op-amp copies the voltage drop VC across the capacitor and adds it to the input voltage VIN to compensate for VC; as a result, the current does not depend on Vc. The copy is used as an output voltage; so the load does not affect the input current because it is supplied by a separate voltage source.
The op-amp serves as a “helping” voltage source VC connected in series to the capacitor.

But if you still want to know the whole truth about the famous circuit, I recommend you read my story below. I have drawn a series of three pictures to illustrate it.

Revealing the circuit contradiction

When we try to improve а circuit, at one point we encounter a contradiction. For example, in the OP's humble RC integrating circuit - Fig. 1, on the one hand, the input source "wants" the voltage drop across the capacitor to be negligible so as not to affect the input current (as other comments also note). However, on the other hand, the next stage "wants" this voltage to be large enough to function properly.

Fig. 1. An RC circuit acting as an imperfect integrating circuit

Solving the contradiction

Basically, there are two ways to solve circuit contradictions - through compromise (used by conventionally thinking circuit designers, engineers, technicians, hobbyists...) and through new idea (used by creatively thinking inventors). The first solution is only a quantitative improvement while the second is a qualitatively new idea leading to invention. Let's consider the two approaches in the OP's RC integrating circuit.

Compromise solution

First, we can moderately increase R, C or both (the so-called time constant R.C) so as not to allow the output voltage to increase much. Thus we will make a trade-off between the linearity and magnitude of the output voltage… but we cannot expect a great result.

Another straightforward solution is to significantly increase the RC time constant and then to amplify the signal… but this will increase the noise as well. Obviously, we need a more clever idea...

Inventive solution

The clever idea. We can borrow this idea from life where we compensate for losses through equivalent income. In this case, voltage drop VC across the capacitor is such a loss because it is subtracted from the input voltage VIN and an effective voltage VIN - VC remains in the circuit. It creates a gradually decreasing current I = (VIN - VC)/R that is less than the desired constant current I = VIN/R.

Conceptual circuit. Following our philosophy of life, we decide to compensate for the "harmful" voltage drop VC by adding an equivalent voltage VC to the input voltage. For this purpose, we connect the following voltage source in series and in the same direction to the input voltage source - Fig. 2.

Fig. 2. The following voltage source VOA = VC adds its voltage in series to VIN thus compensating the undesired voltage drop VC.

Its voltage is added to VIN: so it compensates for VC and the current does not change when the capacitor charges - I = (VIN - VC + VC)/R = VIN/R. As a result, the contradiction is solved and we obtain a perfect linearity combined with high output voltage.

Op-amp implementation. The compensating voltage source can be implemented by a floating voltage follower… but the ingenious solution of the famous op-amp inverting amplifier can be obtained by applying a negative feedback - Fig. 3.

Fig. 3. In the op-amp implementation, the op-amp output acts as the compensating voltage source (only the negative power supply V- is explicitly shown).

Here, the op-amp adjusts its output voltage to make it equal to VC by observing the difference between them with its inputs and keeping it almost zero. If the op-amp non-inverting input is grounded (this is not mandatory), the famous virtual ground appears at the inverting input.

Conclusion

As you have seen above, the idea behind the op-amp inverting integrator is extremely simple. It is just an improved RC integrating circuit where a following voltage source (like a small adjustable "battery") producing voltage VC is connected in series to the input voltage source to help it. As a result, the voltage drop across the resistor R is equal to the input voltage VIN and the input current I = VIN/R depends only on VIN.

Some history

At the end of my story, I want to share an interesting psychological phenomenon - what are people capable of in the name of not accepting someone else's idea... no matter how simple it is... just because it is nobody's but someone's... To illustrate it, I have arranged in chronological order the main materials that I have published dedicated to this simple but clever idea.

The first guesses about this idea arose in my head in the late 80's but it became clear in 1992 when I sketched it on A5 sheet of paper and added it to my collection of circuit ideas...

Yellowed sheet from my idea archive - in Bulgarian. Translated text: (date 05.07.92) Title: Active integrator explained by "anti voltage". Explanation: The op-amp creates "anti voltage" and applies it in series to Uc. As a result, the current I in the circuit (through C) is constant and equal to I = E/R. The capacitor is linearly charged (Uc).

What was interesting to me was not the idea itself, no matter how clever it was, but to derive universal principles of how to convert imperfect passive circuits into perfect op-amp circuits. I managed to do it in 1997 at a university conference Electronics'97 with my material How to convert passive circuits into active ones and I have been promoting it ever since.

In 2001, my students and I carried out a very interesting experiment in the laboratory using a "man-controlled op-amp" (we made it using a battery and a potentiometer). We chose a large time constant (C = 1000 microF, R = 10 k) so that the voltage across the capacitor was slowly increasing. One of the students was slowly moving the potentiometer wiper in the opposite direction so that to keep zero voltage at the virtual ground. As a result, the potentiometer voltage was linearly changing. Unfortunately, I made only one poor quality photo where the details are not clearly visible.

In 2004, I included this idea in my web course on Basic Electronics.

To make it more attractive, in 2004 I created an interactive circuit builder based on this principle:

Building an op-amp inverting integrator - animated Flash movie, Ruffle needed

In 2006, I created a series of Circuit stories on the whiteboard on my site Circuit fantasia and dedicated a few stories to this principle:

How do we build an op-amp RC integrator?

Ramp generator

In 2008, I carried out my next web didactic experiment by uploading the laboratory classes with the participation of my students in the wikibook Circuit Idea. Here is my story about the integrator:

How to make a perfect RC integrator

In 2009, I generalized this principle into a philosophy about all op-amp inverting circuits and created Voltage compensation Wikibooks story. In the talk page I told the history of this idea.

In 2010, I was able to combine this principle with the opposite bootstrapping and to generalize them through the Miller theorem in Wikipedia:

Miller theorem

In the following years, I was popularizing the idea many times in forums including SE EE. Here are some of my materials:

2011 What is the purpose of the opamp in an integrator circuit? - SE EE

2013 Can we virtually increase the capacitance up to infinity? - ResearchGate

2015 My understanding of RC circuits is broken - SE EE

2020 How does an op amp integrator work? - SE EE

2020 Charging of capacitor in RC circuit - SE EE

2021 What does a capacitor do? - SE EE

... until now... a total of 30 years...

And what do you think was the result?

The same as here, in the comments and chats under this question... and what it will be like after my next attempt to show how simple the idea behind the op-amp integrator is... and behind all inverting circuits with negative feedback - just a small "battery" in series to the capacitor...

@Newbie, Any question? Is the small "battery" in series to the capacitor understandable to you? — Circuit fantasist, Jun 20 '21 at 20:11
@Newbie, If you were my student, I would ask you the following question to check if you understood the clever idea: "The capacitor C subtracts a voltage drop VC from the input voltage while the op-amp adds voltage VC to the input voltage. Then what element op-amp represents? What can you call it?" — Circuit fantasist, Jun 21 '21 at 14:24
@Newbie, Yes, you really can name it "compensator"... but try to find a simpler name... like an electrical element having an opposite behavior (ordinary passive electrical elements consume power while this element produces power). — Circuit fantasist, Jun 21 '21 at 14:31
@Newbie, Yes, it can be considered as a kind of battery but *varying battery*... Maybe this [RG question](https://www.researchgate.net/post/Does-the-op-amp-in-all-the-inverting-circuits-with-negative-feedback-behave-as-a-negative-impedance-element-negative-resistor-capacitor-etc) can give an idea how to name it? — Circuit fantasist, Jun 21 '21 at 14:39
@Newbie, You asked me above, "I am not sure what you mean by that I do not react?" and I clarified what I meant. Here again I need your reaction to make an interesting and unusual explanation of this circuit but you are reluctant to react... so I want to explain something else to you... Here and in this world in general, we are not only to take but also to give. I took the time to do something for you and now I need a little help from you. It does not cost you anything to answer my last question so that I can develop my idea that could be useful to some web visitor... now and in the future... — Circuit fantasist, Jun 22 '21 at 20:15
I apologize for the delay. I read the RG question. However, I am not pretty sure on the answer. Negative resistance?? Maybe we can have this extended discussion in chat? — , Jun 23 '21 at 04:48
@Newbie, In particular, here it is a "negative capacitor"... This is just a different point of view on this phenomenon... figuratively speaking... Don't go deeper if you are not interested. My remark was more to the "sages" here but, as you can see, they hide and are silent... Watch and learn how life is so that you are not surprised in the future by inadequate reactions... Thus you will gradually become a "practical psychologist" who sees the "other truth" about people... Thanks for the support. — Circuit fantasist, Jun 23 '21 at 06:15

score 2 · Answer 6 · answered Jun 17 '21 at 12:22

Integrators without op amps are only an approximation.

Consider an ideal integrator with a time constant of 1 second. Put a unit input to it, and the output will rise (theoretically forever) at 1 per second in a perfectly straight line.

Now use an op amp with a 1 Mohm input resistor and a 1 uF feedback capacitor. For a 1 volt input, the output will rise (well, fall, actually) at 1 volt per second. It will do this until the output gets close to the supply voltage, at which point it will limit. Within the limits imposed by the power supplies the circuit will act like an ideal integrator.

Finally, consider a 1 Mohm resistor connected to a 1 uF cap, with the voltage across the cap being the output. If you apply 1 volt to the resistor, the voltage at the cap will initially rise a 1 V/sec. Integrator, right?

Well, keep watching. Instead of rising without limit, the capacitor voltage will start levelling off and will never get above 1 volt.

So, as long as the capacitor voltage doesn't change appreciably, a passive RC integrator works fine. The larger the output voltage, the farther it deviates from ideal behavior.

Really, it is a very good idea to explain in parallel, with the same values of the RC elements, 1) the "bad" (RC) -> 2) the perfect (real op-amp) -> and 3) the "ideal" (ideal op-amp) circuit. But an even better idea is to show how 1 turns into 2 which, in turn, turns into 3... because everyone can see that the active op-amp circuit contains the passive RC circuit. Uncovering the evolution of a circuit solution can best explain it... — Circuit fantasist, Jun 17 '21 at 17:28