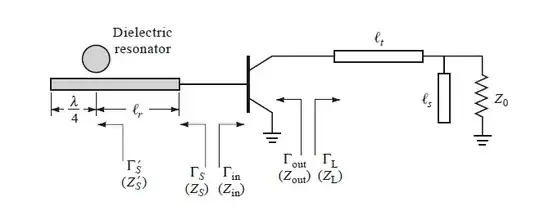
In this post, akellyirl wrote:
As a rule of thumb for design simplicity, the \$G_2H_2\$ loop is designed to be stable with significantly higher bandwidth than the final loop bandwidth so that its phase delay can be neglected in the design of the outer loop; i.e. its phase/magnitude contribution to the overall loop is negligible at crossover.
Is it possible to express that idea mathematically?