What is physically happening when there is a square wave input on the left plate of a capacitor and open circuit on right plate of a capacitor?

Question

Mathematically I understand that through KVL that the output in the first image will match the input square wave. I am trying to understand physically what is happening. How is the voltage transferring across from the left plate to the right plate?

-As far as I understand, there isn't any current flow from the source to the left plate of capacitor

-If there is no current flow, how can charge build up on the left side to create an electric field and push out charge on the right side?

-What is the difference between the first picture with a capacitor and the third picture with an open circuit? Why is it that the voltage transfers in the first picture, but it doesn't in the third where Vout is 0 V. Is it related to the capacitors ability to store charge? If so, why does this matter as in the first picture the capacitor is not holding any charge as it's never charged due to a lack of current. And the lack of current is due to lack of a path for the current to flow to ground.

This has been my one main problem in understanding how charge pumps work.

I guess I am trying to figure out what is the difference between an open circuit and a capacitor. Can't you say that an open circuit is just a negligible non-zero capacitance? As the capacitance is dependent on the plate area, dielectric material, and distance, with two-point wires in an open circuit, the capacitance simply becomes infinitesimally small, but non-zero. If so, what is it about capacitors that the voltage can pass from the left to the right plate, but in an open circuit it can't. Is there some arbitrary capacitance beyond which you see coupling in the real world, maybe?

Answer 1

The Question

You write at the end:

As capacitance is dependent on plate area dielectric material and distance, with two point wires in an open circuit the capacitance simply becomes infinitesimally small but non-zero. If so what is it about capacitors that the voltage can pass from left to right plate but in an open circuit it can't. Is there some arbitrary capacitance beyond which you see coupling in the real world, maybe?

Electronics operates at a model level that sits above where your question is at.

Your question is like asking why it is that 4 times 5 is 20. Most answers will form around the idea that adding up 4, 5 times, makes 20 or that adding up 5, 4 times, makes 20. None of the answers will dig deeper until you ask that question to a specialist of such questions, namely an abstract mathematician.

Electronics, at the level most try to gain it, assumes certain ideas into place. While they are true enough at the level needed, these devolve into circular arguments when you ask why they are what they are. Your question needs to be handled by a specialist of such questions, namely an experimental physicist.

So this really isn't the right place unless you are lucky enough to find one here. I'm not one. So anything I attempt to write will be built from ideas I believe I've acquired correctly, but may not have. Trust nothing I write, but if anything instead just use it to help you better shape your own questions.

A Thought Experiment

Suppose an experimental setup like this:

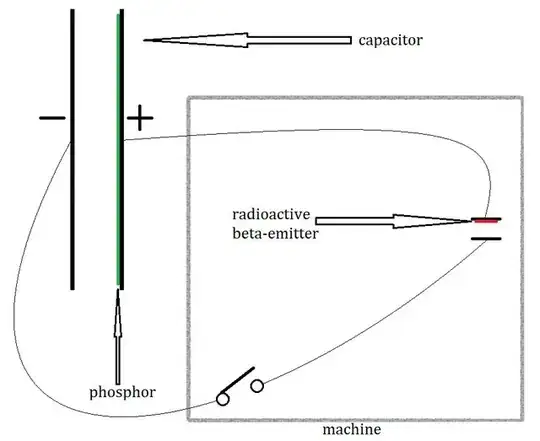
(Click it to make it larger.)

Here, there is a small machine on the right side where we've painted the surface of a small metal plate with a radioactive beta-emitter (emits electrons.) We've managed to design both small metal plates in some fashion (not shown) so that the emitted electrons are entirely absorbed by the plate opposing the painted one. The machine also includes a switch, which will be initially closed for a period of time long enough that the capacitor is charged up to some accelerating voltage.

(We assume for these purposes that the plates can be mysteriously held apart and either kept with a fixed separation or else adjusted so that the separation can be changed without losing their orientation. This assumption is needed for two reasons. The first is that an accelerating voltage between the plates may accelerate the plates towards each other and we need to prevent that. The second is that we need to be able to adjust their separation in this experimental process below.)

As these beta particles accumulate on the opposite surface inside our machine, they diffuse out into the non-radioactive plate. Because it is a metal in this thought experiment, all of the electric charge within the volume of the non-radioactive plate, the conductor leading through the closed switch, and the left plate of the capacitor will distribute itself as a unit (through repulsion) to be evenly distributed, except for a very tiny excess surface charge (because charges near the surface are not repelled equally from all directions, anymore.) So the surfaces of the left capacitor plate, the wire leading to it, the switch itself, and our non-radioactive plate in the machine will all carry a net negative surface charge that is related to this idea of an accelerating voltage.

Meanwhile, as the radioactive plate is losing beta particles, it is equally acquiring a net positive charge. And the same rules apply here, as well, so that the surfaces of the right capacitor plate, the wire to it, and the radioactive plate in the machine will all carry a net positive surface charge that is similarly related to this idea of an accelerating voltage.

We can measure this accelerating voltage, by adjusting the above experiment so that we can make observations of it. We can paint the surface of the positive capacitor plate with a phosphor that will generate light when electrons strike it in just such a way that the light intensity is proportional to the energy released when th electrons strike it. We don't need to know how this phosphor works. It's enough to accept that such a phosphor exists, in principle.

In addition, we've "calibrated" our phosphor by creating, separately, a special gun that shoots "one Coulomb" of charge, with a known mass, \$m_c\$, and with a known velocity, \$v_c\$. We can compute the bullet's kinetic energy using \$K=\frac12 m_c\cdot v_c^2\$. We've used this gun and shot enough bullets into the phosphor that we can detect when a duplicate bullet from some other mechanism (our thought experiment) strikes the phosphor. I'm not suggesting here that we can measure different bullet energies. Only that we can detect if this particular bullet energy occurs.

At some point in time, we open the switch and insert a perfect beta-absorber in between the tiny plates within the machine and we now inject and release a charge of exactly one Coulomb (we learned how to make a one Coulomb bullet for the earlier gun) just at the surface of the negative capacitor's plate. (We hired an experimental physicist to design the details.)

This charge will be repelled by the negative surface charge (the plates are sufficiently large in area that the injected charge "sees" the surface effectively reaching out to infinity away from it) and accelerates directly towards the positive surface charge at the positive capacitor plate. When it strikes that plate, the phosphor will react to the impact.

We can detect when the same pulse of light is received such that it matches up with our known-case of the gun's bullets used to calibrate the experiment. The plate separation is adjusted until we detect exactly the same pulse from the phosphor when the injected Coulomb charge impacts it.

Once this is completed, we can then measure the final, adjusted distance, \$d\$, between the plates that achieved this. Since we know the kinetic energy \$K\$ must be the same as our bullets, now, then we can find the accelerating force such that \$a=\frac{K}{d}=\frac{m_c\,\cdot\, v_c^2}{2\,\cdot\,d}\$. This force is like gravity on the surface of the Earth. It's constant (for the experimental purposes) and ever-present.

Now we have only one thing more to do. We define this experimentally determined acceleration force by another term, voltage, where \$V\propto a=\frac{K}{d}=\frac{m_c\,\cdot\, v_c^2}{2\,\cdot\,d}\$. We can say \$V= \lambda\cdot \frac{m_c\,\cdot\, v_c^2}{2\,\cdot\,d}\$, where \$\lambda\$ is some constant related to our experimental setup.

So, voltage is an equivalent to what sets up potential energy here on Earth.

Summary

There are other details to ask.

For example, what happens to the plates themselves when a bullet is injected and released in this experiment? Obviously, that charge is absorbed by the positive plate and this might change the accelerating voltage, for the next bullet. But we can repair that error by reconnecting the switch until we detect the same bullet energy. In fact, we can arrange the experiment as a closed-loop experiment in such a way that we turn the switch on and off over and over so that our bullets provide exactly the same impact every time.

Or, what if we had to separate the capacitor's plates by a large distance such that it required a light-minute's distance of separation? In this case, we can assume that just prior to releasing the charged bullet, that the positive plate's charge has had enough time to be felt near the negative plate and that the acceleration away from the negative plate would start immediately towards the positive plate, just as before. However, the closed-loop nature of our experiment would now change. It would "take time" for us to "detect" the energy of the arriving bullet and then control the switch to make adjustments. It would also "take time" for the charges being "generated" in the machine to diffuse out and equally distribute to the plates with such a far separation. And when those charges do eventually diffuse sufficiently, it will take time for the changes on the positive plate to be "felt" at the negative plate. These delayed reaction times are what is called magnetism and what defines the effects of magnetic fields. Maxwell's equations are classical, pre-Einstein, and do not take cognizance of the special or general theories of relativity. And, as a consequence, one is required to observe a magnetic field effect in order to bring things back into consistency with experimental observation.

Suppose you disconnect the machine from the capacitor, once the system was calibrated so that there was this fixed accelerating voltage between the plates. (We will assume that the amount of charge on the negative and positive plates is very large by comparison with the bullet's charge for the purposes of releasing one more of them.) We now want to move the plates to change their separation distance and then release another bullet. It will take work to move the plates further apart and we'd get work if we move the plates closer together. But either way, we can do this. The question is, what happens when the bullet is again released?

We will observe the exact same pulse of light, as before. This is because, while we have changed the acceleration itself, the changed distance also changes the experiment's \$\lambda\$ value in just such a way that the energy of the accelerated bullet remains the same on observation. Because of this observed fact, the idea of voltage is a useful one. (In a different universe, it may not have been so useful.)

Now, let's return to your question. Suppose we have any particular capacitor with any particular charges (keep them equal and opposite to avoid drawing out this question more than it already is) on the opposing plates. This defines an accelerating voltage for us. If you connect up one plate to a driven source (by definition a voltage only carries meaning when it is between two plates of metal and therefore must itself have it's own "separate plate" somewhere else), the charges don't change between the plates. So the accelerating voltage doesn't change between the plates (you can still drop that bullet in between them and observe that same pulse of light.) So the voltage between the disconnected side of the capacitor and the hidden plate of the voltage source must itself change when the source's differential changes.

No current is required, here. (Until we decide to release a bullet, of course.) But now if you somehow arrange this new experiment such that you could release another bullet of charge so that it accelerates from the disconnected plate of the capacitor towards the hidden plate of the source, then you would find a different resulting phosphor energy release if the source voltage were non-zero.

Changing the circumstances so that you have a "square-wave" only means that the voltage source has two different states of being. But this doesn't change how to think about the results. You would see the square-wave, plus whatever voltage is on the capacitor, at the opposite, disconnected end of the capacitor if and only if you performed the experiment of releasing those bullets in each of the two different states for the source. And even then, you could only compare this with these two different energy releases against each other or against the energy release measured at the capacitor. You would not have an absolute value.

The absolute values we use for the different accelerating conditions come from chemistry. These values are really just another relative measurement, though. The standard electrode potentials can be experimentally determined, for example. Luckily for us, chemical batteries are able to maintain (through what ultimately comes down to quantum behaviors) a fixed potential difference between two plates of metal.

Additional Pondering

It was Galileo who first realized (so far as we are aware -- keep in mind that Galileo wrote a lot and was ever a self-promoter) that a ball of mass would continue to roll at the same velocity on a flat plane, forever at the same speed and direction.

No one else tumbled to this idea, earlier. But it arrived for him from experiments where he was timing and measuring rates of speed for balls rolling down inclined wooden troughs. He found that when he worked hard to shape and polish his troughs that there seemed to be no angle at which the ball wouldn't roll. The only reason he found for the ball sitting still was some defect in his trough and not something else. By projection, he could "see" where all this was pointing him. And he wrote it out to tell the world.

Suppose a point mass in a universe of only one point mass. What is the meaning of velocity? What is the meaning of acceleration? Does it have one? Can you measure it? Is the universe itself some kind of space-time that is fixed and rooted into something even deeper below, upon which we could measure a velocity or acceleration as an absolute value? (No, the universe isn't rooted in something else and there would be no meaning whatsoever to the question in this case. Nor would you be able to observe any of the special or general theories of relativity, which themselves only arrive out of the existence of interacting particles and forces.)

Now suppose you decide to separate this point mass into two point masses placed at a fixed separation. We can detect the fact that there are two points. But can we measure the distance between them? All we can really do is say, in a topological fashion, that they are not the same as a single point. The distance between them isn't measurable because we have no reference.

It takes a third point in this universe for us to develop the concept of a measurable distance. We can only then begin by measuring the ratio of one distance to another.

This is not unlike what was just done earlier with the capacitor experiment, when adding the idea of a voltage source connected to one side of the capacitor. In the capacitor's case, we cannot measure the concept of an absolute voltage with just the two plates of a capacitor. We can measure the existence of the light pulse and continually adjust the experiment so that the pulse is then detected. But we cannot compare it to anything else until there is a third plate. (This is that hidden plate for the voltage source.) Once a third plate exists, though, we can start to make relative measurements that say "this is so and so many times as much as that is."

So your question is actually a pretty good one.

Answer 2

When I was at school (about 1980) we did a number of experiments using a gold leaf electroscope, which I found very useful at an intuitive level and I would recommend following that up if that's the kind of thing that works for you. In those days it was described like this: you apply a positive voltage to the first capacitor plate, and this has the effect of drawing some of the electrons out of the plate. Electrons are moving out but nothing is going in, so the plate becomes positively charged and attracts the electrons from the second plate. These can't jump the gap (in reality a handful will but we try to ignore these) so instead they congregate on the side of the second plate nearer to the first plate, leaving the rest of the plate (and presumably the wire attached to it) short of electrons and therefore positively charged. If you provide a source of electrons, for example by touching the wire with your finger, some electrons will flow into the second plate to restore the normal balance (1 electron for each proton in the plate). And so on - if you can get hold of an electroscope there are many party tricks that you can do with it.

Answer 3

One of the capacitor ends is floating so there is no completed circuit for current to flow, so no charge builds up. So there will always be 0V over the capacitor terminals.

So if left terminal is set to some voltage by some square wave or other signal, the right terminal will also have that same voltage, because there is always 0V over the capacitor and it cannot get charged.

Answer 4

The reason you see a voltage in your first picture is because in SPICE, dangling nodes have a hidden (very high) resistance to ground. That is because the matrix solver has problems with elements that don't have currents, and that resistance ensures a DC path to ground with a small enough current not to influence the rest of the circuit, but enough to make the engine run. You can't see it, but it's there (usually with the value of gmin). That's why you can see a voltage after the capacitor. If you'll want to probe the current through the capacitor you won't be able to because the solver "knows" that there should be no current through it -- it's just that the effect of adding the gmin from the dangling node to ground means that it's possible to have a voltage where there shouldn't be one, that's all.

Otherwise, if you were to probe the voltage in real life, you would still have some sort of input impedance of the device that performs the measuring, therefore you would still see something. Even open air has a finite resistance.

But if you mean the strictly theoretical aspect, then the same voltage will be seen at the floating end, as the other answers explain at large.

Answer 5

In the first picture the open circuit on the right hand side of capacitor can be considered to be a very large resistance. As the capacitor's left plate voltage rises, the current through this very large resistor (capacitor charging current) is equal to Vout/(very large resistance). Therefore the charging current is negligible, the capacitor hardly charges at all, and the right hand plate stays nominally at the same voltage as the left hand plate. Because the capacitor has significant capacitance, a significant current flow would be required to charge it and create a voltage difference between the plates.

In the third picture there is negligible capacitance between the two wires and so when the left hand wire rises in voltage almost no current is required to charge the negligible capacitance and the very high input impedance of a voltmeter connected between the right hand wire and 0V is sufficient to hold the right hand wire at 0V.

It is important to appreciate that no conduction current (apart from a very tiny leakage current) flows between the plates of a capacitor. When current charges a capacitor, positive charge flows on to one plate and off of the other plate. The process is reversed for the discharge. So, the magnitudes of the currents in the two leads of a capacitor must always be equal to each other, one in and one out or one out and one in. I have used conventional current flow (positive charge) to describe the charging action rather than electron flow as I think it is intuitively easier to understand.

Even with an ac signal, contrary to popular belief, no conduction current actually flows between the capacitor plates (apart from a tiny leakage current). What actually happens in the case of ac is that the currents in the capacitor's leads are continually changing direction and charging and discharging the capacitor (the two currents being equal value and always one in, one out). How much the capacitor actually charges and discharges on each cycle depends upon the size of the charging current, the size of the capacitor and the frequency.

Answer 6

To answer the question directly, in physical space there is no difference between an open circuit and a capacitor; by a capacitor is meant a two-terminal device whose capacitance is relatively large compared to the stray capacitances around it. In SPICE, there is no physical space, so it cannot even define the capacitance of an open circuit, the model simply does not account for such things.

Floating wires are always difficult to conceptualize when you're first considering them. Some things are generally true, notably, if you have a floating conductor, it will be electrically transparent, assuming it is electrically neutral. That is, assuming you didn't actively charge up the conductor, e.g. by electrostatic induction, it will not change the electric field. It will also experience zero net-force. It seems unintuitive, but it is readily apparent from the 'electrically neutral' assumption. (It can, however, be polarized.)

There are more considerations for floating wires, but the question I think you want to ask is: what is capacitance? This is a deceptively difficult question to answer, as most sources don't provide adequate definitions. If we understand capacitance, we will understand what effect it has, and we can better understand why two conductors with some amount of capacitance between them will behave in a certain way.

Here's a start. Consider a conductor in free space. The self-capacitance is the ratio of the electric charge of the conductor to the electric potential (voltage) of the conductor relative to a point at infinity (or generally relative to a point of zero potential). That is, a conductor with capacitance C, when charged to a charge Q, will have a voltage of $$ V=\frac{Q}{C} $$ This is a definition, and it happens that a conductor's self capacitance is independent of charge or voltage (ideally anyway) so it stays constant.

Now we wish to consider the effect produced when a second charged conductor is brought close to the first; a change in potential (even though the charge remains the same) occurs, and this effect is called mutual capacitance.

The multi-body theory of capacitance reveals more details, so I'd recommend looking more into it. But most references are lazy. Maybe later I will edit this to provide more detail. Good luck!

Answer 7

Mathematically I understand that through KVL that the output in the first image will match the input square wave. I am trying to understand physically what is happening, how is the voltage transferring across from left plate to right plate?

Your simulation is just a mathematical model. Nothing is physically happening in it. Its behavior is solely determined by the mathematical equations used in the simulation. So why is the voltage the same on both sides of the capacitor? The Vout side is an open circuit, so (in electrical theory) no current can flow. If no current can flow then the capacitor (which is also defined by mathematical equations) cannot charge or discharge, therefore the voltage difference must be zero, and Vout is the same voltage as V2.

But what you really want to know is what would happen if the capacitor was a real device, made up of physical materials such as copper plates separated by glass. Copper is a conductor, so electrons can freely move thought it. But glass is an insulator, so logically no current can flow through the capacitor. Except that's not right, because current is defined as the flow of charge - not electrons.

The unit of charge is the Coulomb, which is The electric force acting on a point charge in the presence of a second point charge, as a result of the interaction between their electric fields. Electrons don't have to pass through the capacitor to influence the voltage on the other side. If the electrons on one side are stationary (because no current is flowing) those on the other side will be too because there is no change in the force acting on them.

"But hang on", you say. "How can those electric fields work over a distance with no physical connection? Surely there must be more to it than that!". And you would be right, because the electrodynamic force is actually produced by the electrons exchanging virtual photons which 'jump' across the plates of the capacitor. here's the diagram which explains it:-

"'Virtual' photons?", you say "Does that they mean aren't real?". Well they are just as 'real' as anything else in quantum physics, which is defined by mathematical equations that describe the behavior of the various 'particles'.

So what this means is - whether you are looking an electronic circuit or subatomic particles - the answer is the same. What is physically happening is irrelevant. All that matters is that the math works out, because fundamentally the math is all we have.

Answer 8

Think of the capacitor as of a voltage source with zero voltage. The capacitor does not (significantly) change its voltage when a small current flows through it; here even there is no current flowing. So the capacitor will transfer ("shift") the input voltage variations. This arrangement is used in coupling capacitors of AC amplifiers.

This circuit phenomenon can be generalized for any element (resistor, diode, inductor, etc.) connected with only one of its terminals to one of the voltage source terminals. For example, this explains why a second resistor is necessary to build a voltage divider (see my answer to a related question).

Answer 9

Think of a capacitor as a vessel with a flexible rubber sheet dividing it, as in this illustration from William Beaty:

The pressure of the water molecules on each side presses through the rubber sheet, on the water molecules on the other side. If the rubber sheet is neutral, not stretched to one side or the other, then the pressure on the left side is equal to the pressure on the right side. If the pressure of one side were to increase or decrease, so would the pressure on the other side. If the rubber sheet is bent then there is a pressure difference between the sides, but still if pressure on one side goes up or down, so too does the pressure on the other side.

Note that the sheet doesn't need to bend for the pressure to change, just as a brick wall doesn't need to move for you to push on it.

Capacitance is similar, except the fluid isn't water molecules but charged particles like electrons and protons which interact directly through the electric field. The charged particles (electrons, protons) on each plate push through the dielectric to affect the charge on the other side. Charged particles can transmit force without touching just like magnets.

Mathematically, we can say the current through a capacitance is equal to the capacitance times the rate of change of voltage across the capacitance with respect to time:

$$ I(t) = C {\mathrm d V(t) \over \mathrm d t} $$

If the current is zero, than the rate of change of voltage with respect to time must also be zero, regardless of the capacitance. Note, the voltage across the capacitance is not the same as the voltage between one terminal of the capacitor and ground.

SPICE assumes the voltage across the capacitor is initially zero (because it assumes the floating node is connected to ground through a very large impedance). Since the current through the capacitor must also always be zero due to the open circuit, the voltage across the capacitor will always be zero.

I guess I am trying to figure out what is the difference between an open circuit and a capacitor.

In the real world (and not in the ideal world of the simulator), there isn't one. Two wires not touching are two plates of a capacitor. Only, their area is small, and the distance between them is large, compared to capacitors you'd normally buy. This means the capacitance is very low. Two pieces of enameled wire twisted together can make a few pF of capacitance.

Because the capacitance of an open circuit is so very low, it takes very little current to create a voltage across it. In most cases this is negligible so we don't bother including the capacitance between two disconnected wires in the schematic, but for some RF, high speed digital, or high impedance circuits this "parasitic" capacitance can become significant and we must start thinking about it.

Answer 10

This answer has been edited significantly to perhaps clarify that the work W done in charging the capacitor is the same as the electric potential energy stored in the capacitor. Voltage is the electric potential. The circuit model shown with an independent source and capacitor is a symbolic representation or schematic for the physical models involving the concepts of electric charge, electric potential (voltage), work, and energy.

This reference:

http://farside.ph.utexas.edu/teaching/302l/lectures/node47.html

Note, again, that the work W done in charging the capacitor is the same as the energy stored in the capacitor. Since C=Q/V, we can write this stored energy in one of three equivalent forms: $$W = \frac{Q^2}{2C} = \frac{CV^2}{2} = \frac{QV}{2}$$ These formulae are valid for any type of capacitor, since the arguments that we used to derive them do not depend on any special property of parallel plate capacitors.

Where is the energy in a parallel plate capacitor actually stored? Well, if we think about it, the only place it could be stored is in the electric field generated between the plates.

The Capacitor voltage:

$$V_C = \frac{Q}{C}$$

Capacitor model with nodes N1 and N2:

N1 ---| |--- N2

When node N1 of the capacitor is coupled to the source as shown in the question the potential at node N1 rises to 5 volts and falls to zero volts as a square wave. Let the voltage at node N1 be V1 and the capacitor voltage be Vc. Then the voltage V2 at node N2 is given by the equation:

$$V_2 = V_1 - V_c$$

where this relation derives from the physical models for electrical work and electrical energy storage in the capacitor. In the imposed reference frame indicated by the ground node = 0 volts when the source potential varies the forcing function changes the amount of work and energy that would be required to produce net positive charge on node 2 of the capacitor.

The floating conductor, isolated from the source or ground node of a circuit, does not support an internal electric field. In a circuit model its potential is undefined since we know nothing about its surface charge or physical relation to the surroundings in terms of electric and/or magnetic fields. If we specify these details then the circuit model would include a capacitor element and not just the symbol for a floating node.

Answer 11

@jonk went to great lengths to say an experimental physicist is required to answer the question. Well, I'm one of those so here goes...

You've asked 2 (nearly 3) different questions:

1. why can a current/voltage sometimes be detected over a floating wire in a) my program and b) real life, despite theoretically being impossible?

2. what's the difference between two plates close together and two wire ends far apart?

I think the other answers have tackled (1), i.e. theory requires everything to function perfectly. More accurately, you could say theory requires your model/assumptions to be complete, but they weren't.

More important is (2). The answer is size. What's the difference between a rubber band and bungee cord? Size.

The best equation to use is

$$C = A\epsilon/d.$$

This means that the wire ends also form a capacitor, albeit a very weak one (tiny cross-sectional area A and large distance d). Note that the epsilon represents the permittivity of air - because it turns out air can support an electric field.

Another useful equation is V = Ed which means that so long as you can create an electric field across a distance, there will be a potential (voltage) even if there is no charge to flow (current).

In reality, there is no such thing as an "open circuit" in air because air can conduct (proof: lightning exists) albeit badly. However you can have an "effectively open circuit" because the capacitance of your wire ends is just too small to detect. Real voltmeters aren't sensitive enough.

Answer 12

If you observe Vout with any normally obtainable physical measurement device, then you will likely see the input square wave.

This is due to the fact that the measurement device will have a non-infinite impedance that will allow some current to flow through it. According to Maxwell’s equations, at any non-zero V2 frequency, an electromagnetic displacement current will flow through capacitor C2, thus completing the circuit.

If you want a physical picture, When V2 goes negative, it will try to pump some electrons into the the “spring load” of C2. The E field from those extra electrons will then repel some other electrons on the other side of the plate. When those electrons end up at Vout, the voltage potential of that node will change. Etc.

Answer 13

Here's a way to think about the capacitor:

The charge Q+ on the upper plate balances the charge Q- on the lower plate. They are equal and opposite and "hold" each other in place.

Even if you press the switch there's no where for the charge on the lower plate to go so the upper charge doesn't move.