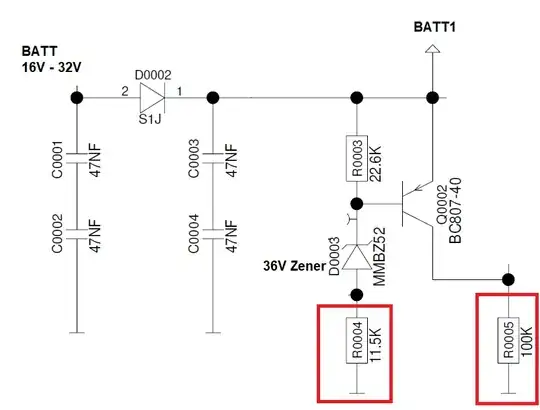
I want to use Thevenin's theorem with the two resistors connected to the base.
How can I combine those two resistors with Thevenin? Do you have any other better idea to combine them? (circled with red in the picture)
(PS: I don't ask the solution of the question. I'm only asking individually the calculation of those two resistors.)