My setup is simply this:
I'll post some slides I made below which explain my issue.
Why doesn't the 700 Hz alias occur if I use the complex data format, but is shown for float data format? I suspect it has something to do with Euler's formula but can't really see it if so.
A real sinusoid \$x(t) = \cos{(\omega t + \phi)}\$, when viewed in the frequency domain through a Fourier transform, consists of two complex sinusoids: one at positive frequency, and one at negative frequency:
$$ x(t) = \frac{1}{2} e^{j \omega t + \phi} + \frac{1}{2} e^{-j \omega t + \phi} $$
The imaginary components of these two terms cancel out and the real components add, leaving just the real sinusoid.
On the other hand, a complex signal generator just yields a positive frequency term \$e^{j \omega t + \phi} = \cos{(\omega t + \phi)} + j\sin{(\omega t + \phi)}\$. In the frequency domain, this is one peak.
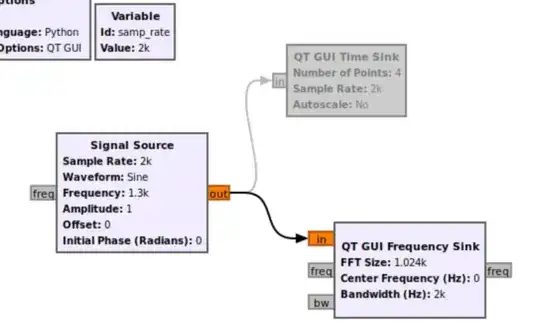
However, I disagree slightly with the wording on the slides that calls this "aliasing" (or am confused by the presentation they use because of a lack of context). Aliasing, in the definition I use, is frequencies outside \$\left[-\frac{f_s}{2}, -\frac{f_s}{2}\right]\$ appearing in that range.
For example, with a sampling frequency of 2 kHz, a 1700 Hz real sinusoid would have a component at +1700 Hz, which would alias to -300 Hz (i.e. 1700 Hz - fs). At the same time, it has a component at -1700 Hz, which would alias to +300 Hz. Likewise, a 1300 Hz real sinusoid would alias its positive component to +300 Hz and its negative component to -300 Hz -- it would look the same as the 1700 Hz real sine because those components are indistinguishable.
