I have this block diagram, and I just can't arrive at the transfer function \$H(s) = \frac{y(s)}{u(s)} \$
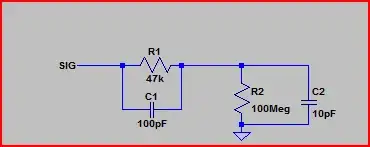
Starting from the end, we see that $$y(s) = xC $$ Let's find out what x is. $$x=\Bigg[\bigg(u(s)-x\bigg)A-y(s) \Bigg]B $$ But as you can see from the equation, it is recursive. I also can't see how the block diagram can be simplified, since nothing is in series or parallel. I hope someone can help me out.