How can I calculate my output and gain when 2 sources are connected at the positive input of opamp?

Question

I can't solve this problem because the opamp's positive input has 2 sources.

How can I calculate my output and gain when 2 sources are connected at the positive input of the opamp?

Answer 1

The Golden Rules of Opamps apply to non-inverting input: no current flows into the inputs of an opamp.

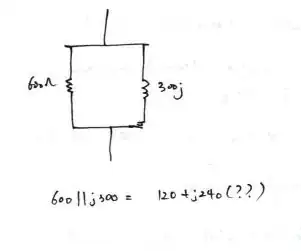
Now, calculating the voltage at the node between R3 and R4 should be very basic network theory!

Answer 2

Perhaps the simplest way is to use superposition (which assumes the op-amp is linear).

By inspection you can see that gain is +151 from the non-inverting input, and -150 from the unmarked voltage source on the left, assuming an op-amp with very high gain.

You can even include input bias current and offset voltage contributions using superposition if you want, but usually problems of this sort ignore input bias and offset currents and input offset voltage.

Answer 3

Perhaps a graphical solution will help you calculate the IN₊ voltage.

^{simulate this circuit – Schematic created using CircuitLab}

Figure 1. (a) The equivalent circuit. (b) A voltage graph.

• The current through R1 is going to run downhill from V1 to V2.
• The total voltage drop across R1 + R2 = V1 - V2.
• The relative voltage drop across R1 and R2 will be proportional to their ratios.
• Now it should be clear from Figure 1b that V+ is two-thirds of the way between 5 V and 3 V.

The rest is a little bit of algebra.

Answer 4

How to analyze circuits

Unknown circuits should be analyzed not blindly as an eclectic mixture of elements but by breaking them into well-known circuit building sub-blocks and concepts.

OP's circuit

Edit: Guided by this "golden didactic rule", we should not consider the OP's circuit as consisting of four resistors and an op-amp but of two sub-circuits - a passive resistor summer (R3 and R4) and an op-amp non-inverting amplifier (R1, R2 and the op-amp).

Passive summer

It is an extremely simple circuit of only two resistors with "magic" properties. It sums the input voltages of single-ended (grounded) sources by pre-scaling them with weighting factors (<1); its output is also single-ended. This circuit is an excellent example of the superposition principle. It can be seen in many other circuit solutions the most famous of which is the inverting amplifier. I have collected related links in my answer to a similar question. The most interesting of them is a Wikibooks story created by my students in 2008.

Non-inverting amplifier

Looking from the side of the summer output, we see a "reversed voltage divider" consisting of an ordinary voltage divider with a gain of R1/(R1+ R2) and a "reversing" op-amp. The op-amp drives the voltage divider input so that to make its output voltage at the inverting input equal to the input voltage at the non-inverting input. As a result, the op-amp output voltage is (R1 + R2)/R1. See more about this explanation in the Wikibooks story created by my students in 2008 and in my RG question.

Inverting amplifier

Looking from the side of the third voltage source (on the left), we can see something very interesting - the two resistors R1 and R2 form the same passive resistor summer as the network of R3 and R4. Here the humble 2-resistor network sums the third input voltage and the op-amp output voltage... and since the latter has an opposite polarity, this is actually a subtractor.

So we can consider R1, R2 and the op-amp not as a combination of two resistors and op-amp but as consisting of a resistor subtractor (R1 and R2) and op-amp. The subtractor is needed for the purposes of the negative feedback (comparison and attenuation).

Two summers

Very interesting... It turns out that we can consider the whole OP's circuit as consisting of two resistor summers and an op-amp? And what does the op-amp do here? It keeps up the output voltage of R1-R2 summer equal to the output voltage of R3-R4 summer.