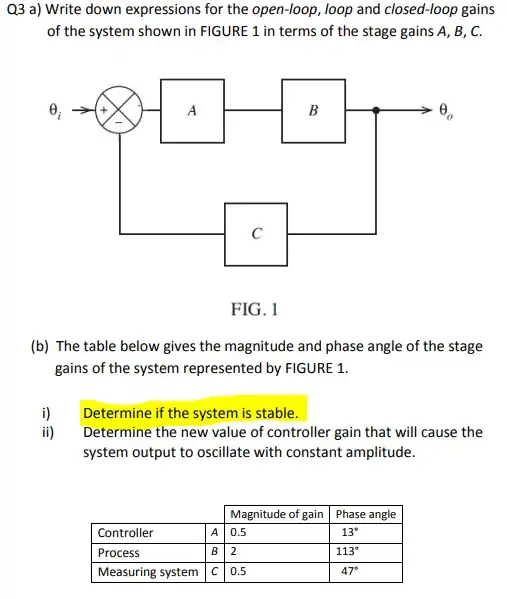
Determine if the system is stable? How is this done? Is this at one frequency? Is the Loop gain is A x B x C = 0.5 Should phase angles be added together = 173 degrees? Should I be considering the open loop or the the loop gain? The only info i have been given in material regarding stability is that at any frequency if the loop gain is greater than 1 and the the phase lag is 180 degrees then it is unstable. The course is only an intro the control engineering but I have no clue where to start with this. The material is terrible and provides very little info.
This is the entire question. There is no other information with it.
Thanks all for your help