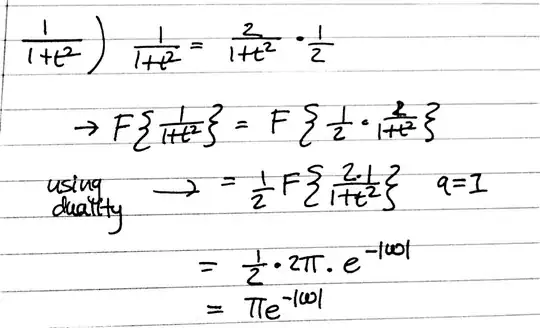Getting the wrong KCL equations in op-amp circuit

Question

I have the following op-amp circuit:

schematic

^{simulate this circuit – Schematic created using CircuitLab}

When I use and apply KCL, we can write the following set of equations:

$$ \begin{cases} \text{K}_1:\text{I}_4=\text{I}_1+\text{I}_7\\ \\ \text{K}_2:\text{I}_7=\text{I}_2+\text{I}_3\\ \\ \text{K}_3:0=\text{I}_1+\text{I}_2+\text{I}_8\\ \\ \text{K}_4:\text{I}_9=\text{I}_5+\text{I}_{10}\\ \\ \text{K}_5:0=\text{I}_3+\text{I}_6+\text{I}_{10}\\ \\ \text{K}_6:\text{I}_5=\text{I}_4+\text{I}_6+\text{I}_8+\text{I}_9 \end{cases}\tag1 $$

In the system of equations, \$\text{K}_6\$ gives the KCL of the incoming and outgoing current from the sources to the ground.

Question: there is a mistake in my KCL equations, but where is it? Because I get the wrong answers.

@MituRaj I explain what \$\text{K}_6\$ is under the system of equations. — Jan Eerland, Apr 30 '21 at 10:29
You don't need an equation for the ground node, and you can't write KCL for an op amp output if you don't consider where that current is coming from. This is the wrong technique for solving circuits like this. Sometimes you need more intuition and can't rely on mathematical software. — Elliot Alderson, Apr 30 '21 at 11:34
K1=K2; K4=K5. The number of nodes should be minimised, not maximised. — Chu, Apr 30 '21 at 11:45
@Jan I would have liked to see what you considered to be "wrong answers." I found no difficulties at all solving this with KCL. All interesting relationships I could imagine were easily found. — jonk, Apr 30 '21 at 19:11

score 3 · Accepted Answer · answered Apr 30 '21 at 20:02

Jan, I won't bother with much (because you can pound out equations as well as the next one) except to say that I wrote the following:

var('r1 r2 r3 r4 r5 r6 io1 io2 vm1 vp2 vm2 vo2 vn i4')
e1 = Eq( 0/r1 + 0/r2 + 0/r3, vp2/r1 + vp2/r2 + vo2/r3 + i4 )   # opa1 (-) input is virtual ground
e2 = Eq( vp2/r1 + vp2/r2, io1 )                                # opa1 output is op2 (+) input
e3 = Eq( vm2/r4 + vm2/r5, vo2/r5 )                             # opa2 (-) nodal
e4 = Eq( vo2/r3 + vo2/r5 + vo2/r6, io2 + vm2/r5 + vn/r6 )      # opa2 output nodal
e5 = Eq( vm2, vp2 )                                            # opa2 (-) = opa2 (+)
ans = solve( [e1, e2, e3, e4, e5], [vm2, vp2, vo2, io1, io2] )

So, for example, I find the impedance seen by \$V_n\$ as:

$$R=\frac{V_n}{I_4}+\frac{R_4+R_5}{\left[\frac{R_4}{R_1\mid\mid R_2}+\frac{R_4+R_5}{R_3}\right]}$$

KCL just works so far as I can tell. I guess I'm not sure what the question might be?

devnull · Answer 2 · 2021-04-30T11:18:18.837

1

K6 gives the KCL of the incoming and outgoing current from the sources to the ground.

Output currents in the op. amps. should not be assumed as coming from the ground. In fact, the power rails are not even considered in the circuit (with ideal op. amps.):

Summary: don't use KCL at op. amp. outputs. Instead, use voltages. The equations should be created considering only the voltages at \$K_3\$ and \$K_4\$. Relying on \$I_8\$ and \$I_9\$ is a problem since they depend on circuits which are not part of the schematic you are analyzing, with ideal op. amps.

Now you can built equations, using Ohm's law, for \$i_1\$, \$i_2\$ and \$i_5\$. E.g.:

$$i_5 = \frac{V_4 - V_3}{R_5}$$

$$i_5 = \frac{V_3}{R_4}$$

[...]

and so on.

Another issue: the circuit forces the two inputs of the first op. amp. to different voltages. This breaks the ideal op. amp. model. Maybe there is a resistor missing or misplaced in the schematic?

Edit: disregard the last paragraph. The new schematic you posted, with an ideal current source, solves the problem as it only forces the total current to the three input resistors. Now you can consider \$V_1 = 0\$ (@ \$K_1\$) for your new equations.

edited Apr 30 '21 at 11:18

answered Apr 30 '21 at 10:22

devnull

8,447
2
15
38

Thank you for your answer. So what am I doing wrong? What equation is wrong and what should it be? – Jan Eerland Apr 30 '21 at 10:28
K6 is not correct. I'll add a figure do my answer as an attempt to improve the explanation. – devnull Apr 30 '21 at 10:31
Okay, but what should it be? Because if I remove that equation I can not solve for all the unkowns. – Jan Eerland Apr 30 '21 at 10:31
Done. Please let me know if it is better now. – devnull Apr 30 '21 at 11:02
I made a mistake in the circuit, the left power source is a current source. But I still do not understand why I can't use KCL. – Jan Eerland Apr 30 '21 at 11:04
1

I'll try to rephrase what is written after "Summary". An ideal op. amp. is a component abstraction which has a single pin sinking or sourcing current from you circuit. How could you use this current to "zero" the currents using KCL if it is not coming from or going to anywhere in the circuit? You are breaking the KCL premise: components don't put or remove currents in the system. It must be a closed system. You can use the currents if you replace the ideal op. amps. by the complete circuits inside them, with power rails. – devnull Apr 30 '21 at 11:11
So, if I complete the circuit with the power rails what should the equation be I need to get? – Jan Eerland Apr 30 '21 at 11:17
You can't just complete the circuit with power rails. You would need the replace the ideal op. amps. by their full circuit with hundreds of components. That is the reason we don't do it. You may also replace them with a better approximation which considers a voltage controlled output and finite gain. What would still be an overkill just because you don't want to built the missing equations using voltages. I'm assuming that if you used ideal op. amps. in the first place, is because they are enough for your purposes. – devnull Apr 30 '21 at 11:24
1

I have asked a similar question before (https://electronics.stackexchange.com/questions/491269/solving-an-ideal-opamp-circuit-leads-to-a-contradiction) and why does it work there and why doesn't it work for this circuit? – Jan Eerland Apr 30 '21 at 11:25

Getting the wrong KCL equations in op-amp circuit

2 Answers2