Thanks for the addition. Just follow these steps:

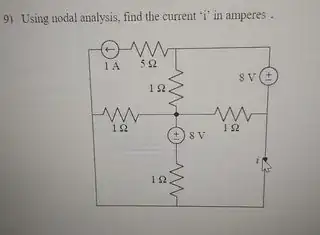
simulate this circuit – Schematic created using CircuitLab
At this point, you've only one unknown node voltage, \$V_x\$, which is now easily computed using nodal analysis (or by simple inspection.) With \$V_x\$ in hand, you can work out all the currents in resistors \$R_1\$ through \$R_4\$.
(The current in \$R_5\$ is obviously already given. \$R_5\$ can be simply shorted out if you prefer, as its only impact is upon the voltage across the current source and no one cares what that is, anyway.)
With all the currents in hand, you can now use KCL on the top-right corner node to work out the current and its direction in \$V_2\$. And then use KCL on the node just above \$i\$ to work out the magnitude and direction of \$i\$.