In a negative feedback loop, why does increase in v_out lead to increase in v-?

Question

I hope this is the right place to ask this question. (Please let me know if there's a better place to ask this.)

Basically, I'm quite confused about how we check if we have a negative feedback loop.

During lecture, when checking whether this was negative feedback, my instructor said that if the v_out increases, then v- increases as well, which would lead to the next v_out decreasing because v_out = A(v+ - v-), where A is the gain of the op-amp. I get how if v- increases the next v_out would decrease and that'd give a negative feedback, but the problem is, I don't understand how v_out increasing (initially) also leads to the v- increasing.

Actually, there was a similar question we went over just before:

For this one as well, my instructor said the same thing; if the v_out increased, then v- also increases, leading to smaller v_out the next time. Here, I thought I understood why: there's a voltage divider from V_s to v_out, where (v- - v_out) = R2 * V_s /(R1+R2). Since none of the resistances nor the voltage source V_s change, if v_out increases, v- would have to increase as well, or that was my understanding. (Is my understanding right?)

However, going back to the circuit for Inverting Summing Amplifier, we don't exactly have a voltage divider, do we? Because the two voltage sources V1 and V2 are in parallel, I don't see how I could combine them (I think you can only combine voltage sources in series). So assuming I'm right in not seeing any voltage dividers in Inverting Summing Amplifier, what makes v- go up as v_out goes up?

Answer 1

You might find the following illustration helpful (but might not!).

^{simulate this circuit – Schematic created using CircuitLab}

Figure 1. Reference circuit for Figure 2.

Figure 2. Picturing the inverting op-amp as a see-saw with it's pivot point being fixed at "virtual ground".

How it works:

• The gain of the see-saw is -2. That means that if we lift the left side by one unit the right side will go down by two units. Note the relative lengths of R_i (input) and R_f (feedback) are in the ration of 1:2.
• (a) With *V_in = 0 V the virtual ground and the output are at 0 V.
• (b) If we raise the input to 1 V we can see that if the output were not to respond that the inverting input voltage would rise to 2/3 V. This would drive the output towards the negative supply voltage rail.
• (c) As the output swings negative balance is restored when V_out = -2 V.

The see-saw analogy works for virtual grounds at non-zero voltages too. e.g. If the non-inverting input is held at 2 V then move the pivot point up to the 2 V line.

---

Non-inverting case - if you're interested:

^{simulate this circuit}

Figure 3. Non-inverting amplifier with gain of 3.

Figure 4. The non-inverting lever.

How it works:

• The left side of R_i is tied to ground.
• When V_in is applied to the non-inverting the output must swing high to bring the inverting input to the same level. This will require the output to go to 3 V in the Figure 3 example.
• The gain of the non-inverting amplifier is given by \$ 1 + \frac {R_f}{R_i} = 1 + \frac 2 1 = 3 \$ which agrees with our illustration.

All artwork mine.

Answer 2

Two answers:

• We have a negative fedback loop when there is one (or three) signal inversions around the whole feedback loop. In both shown circuits, there is one such inversion because the output is fed back to the inverting terminal.

  As another example: We also have negative feedback when the feedback loop contains a second inverting active stage and is connected to the non-inverting input terminal of the main amplifier.

  However, negative feedback applies for the lower frequency region only. As soon as we have additional phase shifts (within the opamp, for rising frequencies) the negative feedback can turn over into positive feedback effects which - in some cases - will cause stability problems.

• Yes, we have a classical voltage divider. For V2=0 the divider ratio is R2/(R1+R2) and for V1=0 the ratio is R1/(R1+R2). Of course, this applies also when both voltage sources are active (because the internal source resistances are zero). In this case, the superposition principle may be applied and the voltage at the in verting terminal is the sum of both voltages which can be calculated separately (and superimposed).

  Comment: The voltage division at the input is independent on the feedback resistor R3 because the inverting input terminal is considered to have a"virtual ground" potential. The resistor R3 becomes effective - in conjunction with R1 and R2 - for the feedback factor only.

(Remark: "Norwegian wood" is one of the finest composition I ever have heard).

Answer 3

You're on the right track thinking about current rather than voltage. It makes understanding op-amp circuits easier. Nevertheless it helps to visualize what's going on. So I've put together a few quick sims to show that.

Quick review. There’s two things at work here.

• Real and 'ideal' op-amp behavior
• Kirchhoff Current Law

Let’s first talk about op amps. There’s two main things that define them:

• very large open-loop gain (in the 10,000’s for real ones, infinite for ‘ideal’ ones.)
• almost no input current (none at all for ‘ideal’ ones.)

An op-amp will strongly amplify any voltage difference between the two inputs. With no feedback, the output will slam to one rail or the other, depending on the polarity at the input. This is open-loop op-amp behavior.

• Open-loop op-amp behavior: Falstad sim, op-amp with direct DC inputs:

The output is either at the max or min power voltage. It's all but impossible to set any pair of input voltages that gets something other than one of the two extremes at the output. This doesn't seem useful at first glance, but it is: it's a comparator. Op-amps can and often are used this way.

Now we'll add negative feedback, that is, a connection between the output and (-) input. The op-amp tries very hard to make the input voltages equal.

• Feedback with with no inputs connected to (-) (simulate it it here):

The output forces the (-) input to the same voltage as the (+) input. This is a voltage follower, or unity-gain amplifier, a useful circuit in itself. The feedback resistor can be any value including zero as no current flows in it.

Now let's look at the inverting amplifier.

• Feedback with 1 resistor input to (-) (simulate it here):

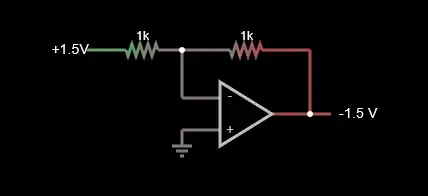
Current flows into the join point at the (-) input. The op-amp sees that slight difference voltage and swings to cancel it, so this inputs remain at the same voltage. As a result, an equal and opposite current flows out of the join point.

You'll also see that the (-) input voltage stays the same as the (+) input. This (-) input is called a virtual ground, as it's created by the op-amp action of cancelling the input difference.

It's not a perfect cancellation though. In the sim the op-amp open-loop gain is set to 100,000, so there's a 1/100,000 gain error. Further, when Vout is -1.5V, there is +15uV at the (-) input. This gain error is present with all real-world op-amps: there will be a voltage between (+) and (-), that is basically -Vout/Av, where Av = open-loop gain. (You can edit the op-amp gain and see the influence.) Nevertheless, for all but the most critical applications this error is acceptable.

(If you're curious about this, here's a discussion: How is op amp output not zero if inputs have the same voltage?)

Now here's where Kirchhoff’s Current Law comes in. The the currents into and out of the (-) input junction point, that is, virtual ground, must equal zero. And, since we also know that there is (almost) no input current in an op-amp, all these currents are via the input and feedback resistors.

What happens when we add another input? The currents into / out of virtual ground add together, and the op-amp feedback dutifully cancels them. The input currents can be into or out of virtual ground; I'll discuss that below.

• Add another input (simulate it here):

Even with current flowing between the inputs, virtual ground is still the same, doing its thing and not moving at all (ok, a little, due to the gain limitation.)

But, how do the inputs interact? This 2-input sim should help you visualize what the input and feedback currents are doing as you try out different input voltages.

• both inputs positive, the currents add, output is negative (sinks from (-))
• both inputs negative, the currents add, output is positive (sources to (+))
• inputs opposite polarity, some current flows between them, output sinks or sources depending on the net difference between them.

So in the 2-input case, each input voltage is amplified, summed and inverted at the output. Yet, each input 'sees' the same voltage: the virtual ground formed at the (-) terminal.

In summary, with negative feedback, the op-amp's strong amplification keeps the (-) pin at the same voltage as the (+) input. This feedback current is the same magnitude, but opposite polarity of the net input currents (that is, their algebraic sum) into virtual ground.

Okay, so let's do some math to show the relationship between input voltages and the output. For the 'ideal' inverting amplifier with (+) at 0V, we have the following current relation between the inputs (I1...n) the feedback current (Ifb):

Current at the (-) input join point, from Kirchhoff's Current Law:

• \$ I1 + I2... + In + Ifb = 0\$

or:

• \$ I1 + I2... + In = -Ifb\$

So:

• \$ \frac{V1}{R1} + \frac{V2}{R2} ... + \frac{Vn}{Rn} = -\frac{Vout}{Rfb} \$

and finally:

• \$ V1\frac{Rfb}{R1} + V2\frac{Rfb}{R2} ... + Vn\frac{Rfb}{Rn} = -Vout \$

The equation gets more complicated if the (+) input is something other than ground. I won't get into it here, but in involves computing the reciprocal sum of the input resistors to determine the noninverting gain. I'm sure your instructor will cover that soon.

Answer 4

Inverting summer

Because the two voltage sources V1 and V2 are in parallel, I don't see how I could combine them (I think you can only combine voltage sources in series).

There are two ways to sum voltages - series (according to KVL) and parallel (according to KCL). In the first case, we simply connect the voltage sources in series while, in the second case, we connect them in parallel but through resistors. Thus we actually convert the voltages to currents, sum the currents and then convert the current to voltage.

In your first circuit of an op-amp inverting summer, the second way of summing is used. Here R1, R2 and R3 form a 3-input passive voltage summer that sums three input (from the summer's point of view) voltages - V1, V2 and Vout. Thus the circuit af an active voltage summer with negative feedback is implemented. It consists of a 3-input passive summer + op-amp... but it has two inputs - V1 and V2, and an output Vout. The role of the op-amp is to make it perfect by creating a virtual ground at the summing point. If you are interested in exactly how it does this "magic", I will explain.

So assuming I'm right in not seeing any voltage dividers in Inverting Summing Amplifier, what makes v- go up as v_out goes up?

The answer should be clear. When in the 3-input passive voltage summer one of its input voltages (Vout) changes ("goes up"), what will happen with its output voltage (V-)? Of course, it also "goes up"...

Inverting amplifier

... there's a voltage divider from V_s to v_out, where (v- - v_out) = R2 * V_s /(R1+R2). Since none of the resistances nor the voltage source V_s change, if v_out increases, v- would have to increase as well, or that was my understanding. (Is my understanding right?)

Let's now apply the same approach to explain the circuit of the op-amp inverting amplifier. Here R1 and R2 form a 2-input passive voltage summer that sums two input (from the summer's point of view) voltages - Vs and Vout. So, again an active op-amp circuit with negative feedback is implemented by adding an op-amp to a 2-input passive summer... but it has only one input - Vs, and an output Vout (it can be considered as a 1-input op-amp summer:) Again, the role of the op-amp is to make it perfect by creating a virtual ground at the summing point.

General idea

Finally, it would be interesting to reveal the role of the summer (subtractor) in negative feedback circuits... to grasp the common idea behind these specific circuit solutions... because this is the way to truly understand them. They tell us that the negative feedback amplifier contains a summer... but we would like to know why. Here is a possible explanation...

Basically, the most elementary negative feedback amplifier can be made simply by connecting the output of an inverting amplifier to its input. As a result, it will keep up zero output voltage.

But we do not have much benefit from such a zero voltage source. We want to control its voltage… to make the circuit an amplifier. For this purpose, we can apply a seemingly strange idea - to disturb the circuit by adding (subtracting) an external (input) voltage. The op-amp will react to this intervention by compensating the "disturbing" voltage with an equivalent voltage… and we use the latter as an output voltage. Voltage followers are based on this idea of compensating an additive disturbance.

Fig. 1. A negative feedback system (Wikipedia)

We can continue in this direction by adding a multiplicative disturbance (beta) in the negative feedback loop. The circuit will react to this new intervention by increasing its output voltage 1/beta times… and will become an amplifier with negative feedback...

---

Note: I used a slightly unconventional point of view to answer your question. I did it to intrigue you and make you think...

Answer 5

The following analysis assumes that the amplifiers are ideal in the sense that input offset voltage is zero and that the hFEs of the input pair are matched so that input offset current is zero.

Case1

For a dc input, Vout must always be slightly more negative than -10 x Vin. The output error is greater the nearer to Vdd the output gets. The small error at the output is greater at voltages closer to Vdd in order to create a larger difference voltage between the bases of Q1 & Q2 which is needed to drive Q5 harder (more base current) to pull the output up to a more positive voltage.

If the output voltage was exactly -10 x Vin then there would be no difference voltage between the bases of Q1 & Q2 and no drive current being pulled from the base of Q5. The output would start to fall until a difference voltage is created between the bases of the input diff pair which holds the output in place all be it with a small error. The higher the open loop gain, the smaller the output error and the smaller the input difference voltage.

Case2

For a dc input, Vout must always be slightly more positive than -10 x Vin. The output error is greater the nearer to Vss the output gets. The small error at the output is greater at voltages closer to Vss in order to create a larger difference voltage between the bases of Q11 & Q12 which is needed to drive Q13 harder (more base current) to pull the output down to a more negative voltage.

For an ac input, the open loop gain of the amplifiers is fixed at a certain value for each frequency and so at any certain frequency, as the output voltage increases (due to an increase in Vin), the difference voltage between the bases of the input pair must also increase because of the fixed open loop gain = dVout/dVdiff.

Put another way, as the output voltage increases, the compensation capacitor (C1/C2) must charge to a higher voltage in the same time period which requires more current out of the input stage. Hence a larger difference voltage between the bases of the input pair is required to provide this current. For ac, the increase in difference voltage between the bases of the input pair is generated by more phase lag at the output (for increasing frequency as open loop gain reduces).

Answer 6

An ideal inverting op-amp amplifier, v- will be at the same potential as v+. Since v+ is grounded in your example, v- will be zero. v- is called a virtual ground. This concept of a virtual ground is due to the high open-loop gain (infinity gain & bandwidth for an ideal op-amp) of the op-amp and is useful for generating a level 1 approximation of the closed-loop gain.

In reality, there is a tiny voltage at the v- input since the gain is not infinity (still a very high number), but you would be hard pressed to view this on an oscilloscope since it's so small unless the frequency is high enough where the op-amp gain is rolling off (more advanced course subject).

While your professor is technically correct, it is an overstatement if looking at an ideal op-amp (infinity gain, infinite bandwidth).