I have been trying to understand what is the trick behind online calculator which gives me CRC value for any input. The thing is that results I get with doing maths by hand do not match results this calculator gives me. On the other hand, I also found this calculator, which always gives the results I get by doing XORing by hand.
Also, I have done my calculations the same way they are done in the following sections at Wikipedia and here. I know I'm doing it the right way, however that calculator (and other ones, like this one) always gives me different results, except for some custom polynomials.
There might be a catch to the way these CRCs are calculated - Wikipedia suggests that there are next following polynomial representations: normal, reversed, reciprocal, reversed reciprocal. And first calculator I mentioned uses two more parameters regarding polynomial: initial value and final XOR value (for purposes of verifying by-hand calculations I chose CRCs with those two values being 0x0).
I'm really struggling to understand if I'm doing something wrong, where some sources say it's done this way, and some other calculators give completely different results then expected.
EDIT:
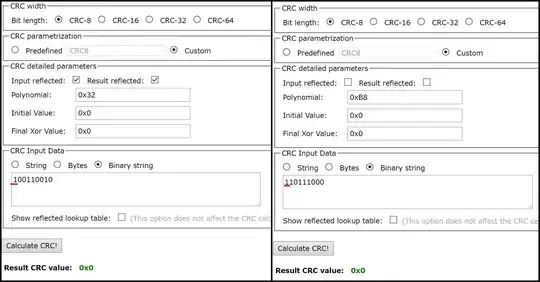
If the message and polynomial are of the same value, then resulting CRC value should be 0, since there is no remainder. This is how I checked that there is some other processes to CRC calculations other then the XORing message and polynomial:
On the other hand, I just found out that (at least) custom defined polynomials ignore the highest term of polynomial (in the case of CRC-8, this would be \$ x^8 \$ which corresponds to 9th bit). This can be verified by inputting message that equals real polynomial (addition of "1" to message byte):
This corresponds to the following quote from Wikipedia:
Omission of the high-order bit of the divisor polynomial: Since the high-order bit is always 1, and since an n-bit CRC must be defined by an (n + 1)-bit divisor which overflows an n-bit register, some writers assume that it is unnecessary to mention the divisor's high-order bit.