Let's consider a capacitor made of a couple of parallel metal strips (suppose they are made of perfect electric conductor) as shown in the figure, which represents a little capacitor.
Suppose an external (time variant) electric field is applied in the space in which the capacitor is placed, as shown in figure.
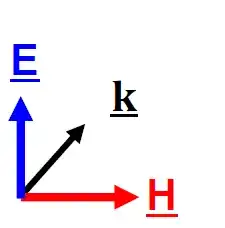
Such an electric field may be for instance that of an incident orthogonal electromagnetic wave, as shown in the following picture.
What happens? I don't know which are cause and effects in this situation.
I'd say that:
The external electric field induces separation of charges in the two strips. So, plus charges on one strip and minus charges on the other.
The previous situation is like that happens on a capacitor when supplied by a voltage source. But, in such a case, I'd say that the voltage source provides charges to the capacitor metal plates, and then the resulting charge distribution generates the electric field. In this case, however, the electric field is already existing since it's the external electric field (the incident wave).
In other words, is the electric field between the plates the original external incident E field or is it the E field generated by the charges separated by the original incident E field?