Is there some rigorous treatment of convergence issues in transient analysis?
I am using LTSpice. In transient analysis with maximum time-step is used. Fundamental oscillatory frequency of analysed circuit is under 100MHz.
I undestand that implicit trapezoidal integration can produce nonphysical ringing. On the other hand Gear algorithm of a given order introduce damping which is also nonphysical. So I tried Gear, trapezoidal and modified trapezoidal implicit integration schemes implemented in LTSpice.
But none of the methods can eliminate these micro-transients.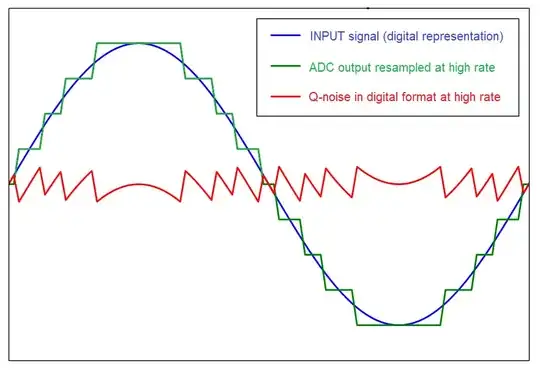
and also note, that they start to showing up after some time.
But I have suspect these are not real oscillations. With Gear I got less of these events.
It is quite simple model of circuit with ideal components (low damping). Its unlikely that real-world circuit will have similar properties, but since I am processing large amount of such transients in Matlab, I need to be sure that I can remove these (using wavelet transform reconstruction for example) as they have no significant effect and are purely numerical product.
What is your rule of thumb for situations like this? Whenever modeled circuit contains LC tanks with much lower frequency than its artefact?
Using equivalent series resitance of 0.1 ohm for shunt capacitances still produce these transients. One can be spotted right on the startup