How do I select the correct inductor value for the following buck regulator?

Question

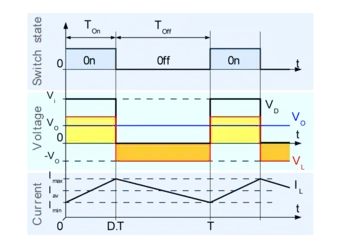
First of all, I suck a bit at math, and I'm no electronics genius, so the stuff I do is for fun and for learning purposes...

I'm working on a buck converter circuit to convert my USB Vbus 5V to 3.3V. I've selected the AP5100 and finding it quite challenging to figure out the correct values on some of the components.

The datasheet neatly specifies the values for R1(49.9kΩ) and R2(16.2kΩ) in Table 1 on page 6, to establish an output voltage of 3.3V, but I'm finding it a bit of a train smash understanding how to calculate the inductance value for the L1 inductor. The datasheet indicates 3.3µH on page 2, Figure 3:

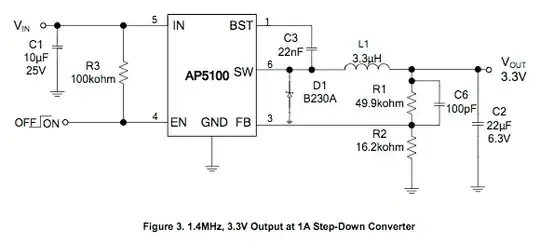
I'm wanting to understand better how the 3.3µH was calculated, and if this is in fact the correct value for my application.

Now back to the datasheet, the formula for calculating L is stated as:

$$ L = \frac{Vout \times (Vin - Vout)}{Vin \times \Delta IL \times fSW} $$

Where ΔIL is the inductor ripple current, and fSW is the buck converter switching frequency.

The datasheet states:

Choose the inductor ripple current to be 30% of the maximum load current. The maximum inductor peak current is calculated from:

$$ IL(MAX) = ILOAD + \frac{\Delta IL}{2} $$

Alright, this is where I'm horribly lost, and trying my best to wrap my tiny brain around the value.

I know the following:

• Vin = 5V (USB Vbus)
• Vout = 3.3V
• fSW = 1.4MHz
• I = 2.4A (I think)

How does one determine the ΔIL (ripple current) in order to get to the inductor value?

My formula should look something like this in the end, right?

$$ L = \frac{3.3V \times (5V - 3.3V)}{5V \times \Delta IL \times 1.4MHz} $$

But what is ΔIL?

Also I thought the buck converter was supposed to allow a range of inputs for Vin, in the case of this one, 4.75V to 24V?

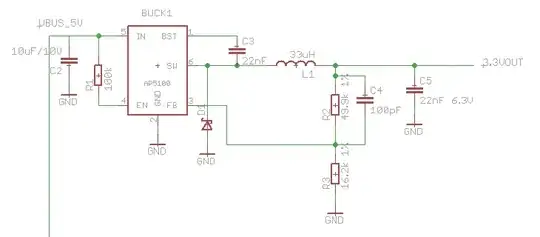
Here's my schematic I'm drawing in Eagle CAD:

Answer 1

Choosing an inductor value for a buck regulator comes directly from V = \$\frac{\text{L di} }{\text{dt}}\$ . Where V is the voltage across the inductor, and i is the current through it. First, you want to design for the case where the inductor is in continuous conduction mode (CCM). This means that energy in the inductor doesn't run out during the switching cycle. So, there are two states, one where the switch is on, and another where the switch is off (and the rectifier is on). Voltage across the inductor during each state is essentially a constant (although it is a different value for each state). Anyway since the voltage is a constant, the inductor equation can be linearized (and rearranged to give L).

• L = \$\frac{V \text{$\Delta $t}}{\text{$\Delta $I}}\$ this is the basis for the equation you saw in the app-note.

• \$\text {$\Delta $I}\$ is something you define, not determine.

You will want to maintain CCM operation, so define \$\text {$\Delta $I}\$ as some small fraction of inductor current (I). A good choice is 10% of I. So, for your case \$\text {$\Delta $I}\$ would be 0.24A. This will also define the ripple current in the output capacitors, and less ripple current means less ripple voltage on the output.

Now you can choose an optimal value of L using \$V_{\text{in}}\$ and \$V_o\$ (and hence the duty cycle D = \$\frac {V_o} {V_ {\text {in}}}\$). But you can also make a quick over estimate for the inductance where you don't consider \$V_{\text{in}}\$ using L ~ \$\frac{10 V_o}{I_o F_{\text{sw}}}\$ (for more on this look here How to choose a inductor for a buck regulator circuit? ). An over estimate can be worthwhile, especially if you are early in development or uncertain exactly how much the output current will be (output current tends to end up higher than expected usually).

Since you are looking at Linear Tech you should (as Anindo Ghosh pointed out) also look at using their CAD support.

Answer 2

For designing a buck regulation circuit, it might be better to start with one of the various free online power design tools on the web sites of manufacturers, such as:

• Fairchild Semiconductor: Power Supply WebDesigner
• Linear Technology: LTPowerCAD
• Texas Instruments: WeBench Power Designer and SwitcherPro Design Tool

By providing your requirements (including acceptable ripple for instance) as parameters, the tool would typically shortlist a set of controllers that meet the purpose. This is usually a safer approach than starting with a controller already decided upon, then attempting to deviate from the datasheet specified values for support components.

Many of the mentioned free "power designer" tools provide a complete bill of materials as an output - including the inductor(s) needed, typically with part numbers.

Some (e.g. TI WeBench) also provide recommended layout and required board space estimates. Some tools further allow desired board space as a design parameter, as also component count, cost, and other preferences.

Answer 3

It might help to understand what happens if you select an inductor of the wrong value.

If you select an inductor with too low a value, the current through it will change too much in each switching period. The current might grow so much in a switching period that it exceeds the current capability of the circuitry driving the inductor. This high ripple current also isn't nice to the capacitor on the output side. ESR losses in the capacitor will be high, or ripple current will exceed the capacitor's rating and it will fail.

If you select an inductor with too large a value, you will be paying for a lot of inductor you don't need. Inductors with a core have a saturation current. This is the current at which the core can not take any more magnetic flux, and the inductor stops being an inductor with a core, and starts being almost a wire. For a given core of a given size and material, you can make an inductor with higher inductance simply by putting more turns of wire around it. But, each of these turns contributes more magnetic flux, so by adding more turns, you are also decreasing the saturation current of the inductor, since your current will be multiplied by the number of turns of wire to arrive at the magnetic flux through the inductor. Thus, if you want a higher inductance at the same saturation current, you need a physically larger core.

I'll leave an explanation of the math to another answer. I'm not the best at such things.

Answer 4

How does one determine the ΔIL (ripple current) in order to get to the inductor value?

Use the rule of thumb provided by the chip maker (select a value that's equal to 30% of your expected maximum DC output current). Also, there's a note on page 8 that says "A 1μH to 10μH inductor with a DC current rating of at least 25% percent higher than the maximum load current is recommended for most applications."

I = 2.4A (I think)

However, it sounds like you aren't sure what your expected maximum DC output current is.

Take a look at this waveform shamelessly borrowed from Wikipedia:

The inductor current is shown at the bottom. The magnitude of the ramps are defined by

\$V_L = L \cdot \dfrac{\Delta I}{\Delta t}\$

You define your inductor by the size of the ramps: that is to say, by choosing a value that's 30% of the maximum expected DC output current (\$I_{av}\$ in the waveform). This is why it's important to know your maximum expected DC output current before trying to choose the inductor.

Also bear in mind that this part has internal error amplifier compensation, which will put constraints on the output LC filter (don't deviate from their inductance range unless you have equipment to measure the closed-loop frequency response of the converter).