Those capacitors are 2 mF and they short the outputs the way you connected them. When you have no load, there's no need to filter the output, but since the filter, after being designed, is likely to stay in place, then you're going to need a proper filter.
For a voltage source sine PWM (SPWM), an LC filter is needed or, at the very least, a series inductor. See this for a quick, asymmetrical filter example: see the way L1 and C1 (in both schematics) connect to form an LC lowpass with Rout as load. When there's no Rout, the lowpass LC still exists, but there is no such thing as a capacitor of (very) large values connected straight to ground. If you only have a series inductor, then without load there will be no current flowing, so you'd see no filtering.
If these things are new to you, it's best to not tackle them as complicated as they are, rather, start simple.
That said, what you have there is an SPWM (sine PWM). In order to make the load see only the modulating frequency (the sine), some filtering is needed. Since this is done on the load side, the filter needs to be passive and lossless: passive because an active one doesn't make sense due to the dissipated powers, and lossless for maximum efficiency. This implies the use of LC elements.
Calculating such a filter is not done in the way the classical passive filters are, but rather with the load in mind, and with the particular topology of the inverter. For a current mode inverter, no matter the order of the filter, the first element needs to be in parallel with the load; for a lowpass, this means a capacitor. For voltage mode inverters -- this case -- the first element has to be in series with the load; for a lowpass, this means an inductor. You can tell when it's current or voltage mode by the DC storage element: for c.m. it's an inductor, for v.m. it's a capacitor; or by the extra series diodes in the bridge. In your schematic, you have no series diodes (only the anti-parallel ones built-in the switches), so it's a voltage mode.

I have drawn the bridge as the books would show them, otherwise choose the appropriate switches for you application. Nowadays, the anti-parallel diodes are built-in.
To filter out the PWM and leave the sine, a lowpass filter is needed, which means that your filter must start with a series inductor. The order of the filter depends on the requirements. Since you don't specify anything, I'll make some assumptions. For the load, in your picture there's a 1 KΩ. For a 325 V supply and with a maximum 90% modulation, this results in a (325*0.9)2/1000 ≈ 86 W peak. Note: the DC voltage is usually chosen to be the peak output sine divided by the maximum modulation, plus some reserve. In this case, 325 V would be the peak sine at the output and the maximum modulation 0.9, so the absolute minimum voltage would be 325/0.9 = 361 V. Add some margin of error and you get what is a more common value in single-phase inverters: 375 V ... 400 V. You have 325 V, so that's what we'll use. The peak current will be 325/1000 = 0.325 A.
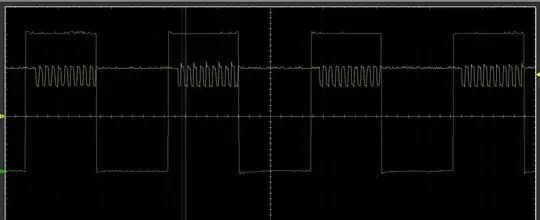
Due to the switching nature of the PWM, filtering it with an inductor will result in a triangular shaped waveform (the blue trace). The inductor is chosen such that the current ripple is some percentage of the maximum peak current; for a 5% variation ΔI = 0.05*0.325 = 16.25 mA. The current through an inductor is \$i_L(t)=\frac1L\int_0^t{v_L(t)\,\text{d}t}\$. We can assume the voltage to be perfectly square, which means the integral becomes a simple difference: \$\frac{V_{max}-V_{min}}{L}\Delta t\$. For a bridge, \$V_{max}\$ is the supply voltage and \$V_{min}\$ is the ground, while Δt is the ON time; for this particular case, the maximum value for \$t_{ON}\$ is chosen, which is related to the modulation index. In the comments you've chosen the switching frequency to be 78.125 KHz (probably from the reference I gave), so with the maximum modulation of 0.9 the inductor is: L = 325/0.01625*0.9/78125 = 0.2304 H. In an ideal world, the huge resulting value would not matter, but in parctice it would mean a heavy, bulky inductor, which will also have considerable losses. This is one reason why a simple inductor is not used in practice and, instead, a minimum 2nd order LC is chosen.
This is how the outputs look like with load and a 1st order filter (simple L, left), and with a 2nd order (LC, right); below, the equivalent schematic of the filter + load, as you would see them drawn in the books:
For this case, the same considerents as above are used: the current ripple through the inductor and the capacitor, but also the attenuation of the frequencies. This is not an wasy task, and there are a lot of studies about this, but one way to start is to select the geometrical mean between the sine and the switching frequencies: \$f_p=\sqrt{f_{sine}\cdot f_{PWM}} = \sqrt{50\cdot 78125} \approx 2\;\text{KHz}\$. Note that this PWM frequency is rather high, because you'll be switching high voltage, though not necessarily high currents. A more common value is up to 10, 20 KHz, no more (it can be in the range of low KHz for high power inverters). Let's assume that the reactances of the LC elements are equal to the load at the corner frequency: L = 1000/ω ≈ 80 mH, C = 1/(ω*1000) &approx 80 nF. The values are still large, so we can cheat by selecting only a quarter of the output load, which results in the LC values being multiplied by 4: 20 mH and 330 nF (a more common value). This is how the powers look like now:
The measurements:
supply: AVG(-i(v3)*v(vcc))=41.1254 FROM 0 TO 0.02
load: AVG(abs(i(rout1)*v(z,y)))=41.0857 FROM 0 TO 0.02
And the output stage with the final values:
Since they're idealized elements, the high efficiency is to be expected. BTW, you're measuring RMS current through the supply, but that's not right: you have a DC voltage and the current drawn will not be sinusoidal; the same for the load. If you would measure the RMS values, you'll discover that the supply current is less than the load.