My professor had told us that Bilateral elements have V-I characteristics which are symmetric about the origin.
In an exam, we were asked to draw the V-I characteristics of a non linear, bilateral element.
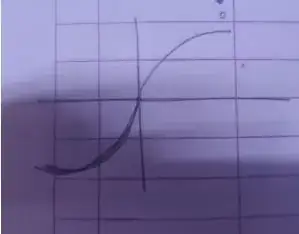
The given answer was:
Shouldn't "symmetric about origin" imply something like this?
Have I misinterpreted the term "symmetric about the origin"? I am fairly sure that in the normal context, this corresponds to curves like my second image.