0

Does anyone have a good: book / link / resource which describes from the ground up how to find an equation / transfer function and the accompanying uncertainties for sensors?

I am looking for references for my bachelor's thesis and want to understand it better myself, what the approach is when designing a sensor how to find the transfer function and calculate the uncertainties.

With my limited knowledge, I understand an equation / transfer function has to be found which describes the sensor Input and Output. This can be done by calibrating the sensor with a lookup table and curve fitting.

This is my approach to calculate the transfer function of my sensor:

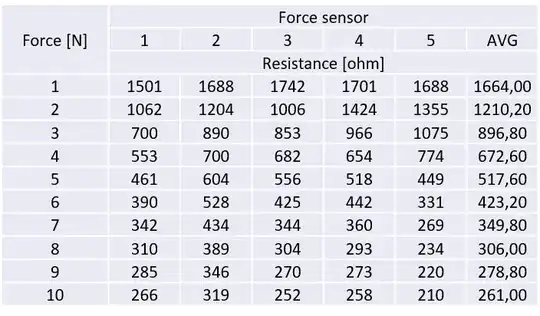
I have a self made pressure (force) sensor which changes its resistance based on exerted force. It acts like a variable resistor. I have measured the resistance of the sensor 5 times at forces from 1 to 10 N, using a digital multimeter. Then I calculated the average resistance at each force level (AVG in the 1st table.)

These averages I graphed, and let Excel make a power function trendline to describe the AVG data. The function and R^2 value is displayed on the graph.

Then to calculate uncertainty:

In the last table I calculated the MAPE (mean average percent error.) Here under "theoretical resistance" are the calculated resistances from the trendline power equation at each force value. I compared the original AVG resistances to this theoretical power function and below are the calculated MAPE and MAE error values.

Is my sensor uncertainty thus the power equation +/- this MAPE of AVG vs theoretical?

  • R = 2008,1*F^(-0,871) +/- 8,2 % ?

circuit table measurement results graph avg vs F table of calculations

BetweenBeltSizes95
  • 57
  • 6
  • This might help you on your way: https://www.physicsforums.com/threads/how-to-find-transfer-function-of-real-world-system.826397/ Summary: You excite the sensor with specific standard waveforms (impulse, step, sine, sweepding sine) and measure the response. Not like how you are doing it which is more of DC calibration and doesn't take into account the dynamic response of the system. – DKNguyen Jan 09 '21 at 22:02
  • Just to clarify: when you say "transfer function" you mean the fixed relationship \$y = f(x)\$, where \$y\$ is the output (resistance in this case), \$x\$ is the input (force in this case), and \$f(\cdot)\$ is the transfer function. You are *not* talking about any time-related phenomenon, like what \$y\$ looks like if \$x\$ is varying rapidly. Yes? – TimWescott Jan 09 '21 at 23:19
  • I don't think your curve is a very good fit. You've got a nice smoothly varying set of dots there; there should be *some* curve that'll fit it better than the one you've chosen. – TimWescott Jan 09 '21 at 23:23
  • Often this kind of resistive force transducer has a significant amount of unwanted temperature sensitivity. It's not enough just to measure resistance vs force, you need to also control for temperature variation. Also, it's customary to configure the force sensitive resistive element as one leg of a Wien bridge, so that the output is a differential signal; that helps eliminate a source of common-mode errors such as the resistance of the power and ground leads. Temperature compensation of force sensors is well known in industry, see Maxim Integrated MAX1458 / MAX1450 / MAX1455. (I work there) – MarkU Jan 09 '21 at 23:56
  • When I was doing this back in 1998 for the MAX1457, industrial quality force sensors had at best 1% repeatability errors, after taking hundreds of measurements using both a temperature chamber and a pressure controller, a pressure manifold, and multiple sample parts, cycling the parts multiple times, and applying compensation; this uncontrollable non-repeatable error inherent in the sensor. Sensor had a Wien bridge configuration, bridge was exited by a current source, so bridge voltage proportional to temperature and differential output influenced by both force and temperature. – MarkU Jan 10 '21 at 00:02
  • @TimWescott yes i mean the function y = f(x), for a thermistor this equation would be the steinhart equation, i would like to know how one goes about finding such an equation for any sensor, so far i have not found any good material explaining this. – BetweenBeltSizes95 Jan 10 '21 at 15:52
  • @DKNguyen my sensor relates force to resistance. I dont understand how putting a voltage sweep across my force sensor would help me determine the sensor "equation". From what i have seen the force needs to be controlled increased and the resistance measured. So i think im looking for resources explaining calibration and uncertainties, not transfer functions of low pass filters etc. – BetweenBeltSizes95 Jan 10 '21 at 16:10
  • @BetweenBeltSizes95 I never said you voltage sweep. I said you excite the sensor which is another way of saying you sweep the *input*. If force is your input, that is what you sweep! My eyes are glazing over just thinking about what would be involved in such a machine. I agree, it sounds to me like you are not looking for transfer functions (which would describe the steady state and transient response of the system to both static and dynamic inputs). – DKNguyen Jan 10 '21 at 17:53

1 Answers1

0

The uncertainty has nothing to do with your theoretical formula. You should measure the force with your constructed measurement device using precise weights - standard. You do increase weight, decrease, mix and you write a table with measurements. Only then, you can determine what's the uncertainty of your instrument.

Observing the uncertainty from indirect measurements has no sense.

Marko Buršič
  • 23,562
  • 2
  • 20
  • 33
  • Im looking for a book / resource which explains how to find the equation and uncertainties for sensors. If my approach was wrong please explain why, im not familiar with the terminology and definitions yet. Is a set of measurements made like i did? is the accuracy given by 95 % / 2 standard deviations of the average results? I have not found good material on explaining all of this. – BetweenBeltSizes95 Jan 10 '21 at 16:06
  • I have a books form university times, but not English Accuracy and uncertainty are different things. . – Marko Buršič Jan 10 '21 at 18:29