Confusion in identifying positive/negative feedback of opamp for a given circuit

Question

I was reading this post How are positive and negative feedback of opamps so different? How to analyse a circuit where both are present? for identifying positive/negative feedback of op-amp circuit.

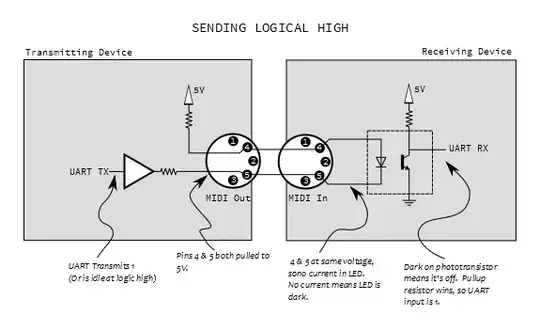
Consider the circuit shown in figure(1):

^{simulate this circuit – Schematic created using CircuitLab}

According to the approach suggested by nidhin:
$$v_-=v_{in}=1.6 \quad (\text{by inspection})$$ $$v_+=\frac{4}{3+4}v_o=\frac{4}{7}v_o$$ Now substituting in the formula: \$ v_{o}=A_{ol}(v_+−v_−)\$ , we get:
$$v_{o}=A_{ol}(\frac{4}{7}v_o− 1.6)$$ $$\implies v_o (1- \frac{4}{7}A_{ol} )=-1.6 A_{ol}$$ $$\implies v_o =\frac{-1.6 A_{ol}}{1- \frac{4}{7}A_{ol} }$$ $$\implies \frac{v_o}{1.6} =\frac{- A_{ol}}{1- \frac{4}{7}A_{ol} }$$ $$\text{so, } A_{cl}=\lim_{A_{ol}\to \infty} \frac{v_o}{v_{in}} =\lim_{A_{ol}\to \infty} \frac{v_o}{1.6}=\lim_{A_{ol}\to \infty} \frac{- A_{ol}}{1- \frac{4}{7}A_{ol} }=\frac{-1}{- \frac{4}{7} }=1.75$$ Now, as \$ A_{cl}\$ is finite , \$ \implies \$ net feedback is negative

But according to the approach suggested by Alfred Centauri:
Assume there is a net negative feedback, \$\implies \$ the non-inverting and inverting input voltages are equal $$\therefore 1.6=\frac{4}{7}v_o$$ $$\implies v_o= 2.8$$ However, $$ A_{cl}= \frac{v_o}{v_{in}}=\frac{2.8}{1.6}= 1.75>0 $$ which is a \$ {\color{red}{\text{red flag}}} \$ since inverting-amplifier should have negative gain
Hence, our assumption is wrong
so according to this approach, net feedback is positive
which is making me confused;
Hence,

1)Identify the net feedback in figure(1) with explanations
2)If the circuit in figure(1) is in net negative feedback, then where did i make a mistake in implementing Alfred's ideas, or
If the circuit in figure(1) is in net positive feedback, then where did i make a mistake in implementing nidhin's ideas

UPDATE:
If we use a non-ideal voltage source \$ V_{in}=1 \$ volt with \$ R_s =1 K \Omega \$ , i.e,

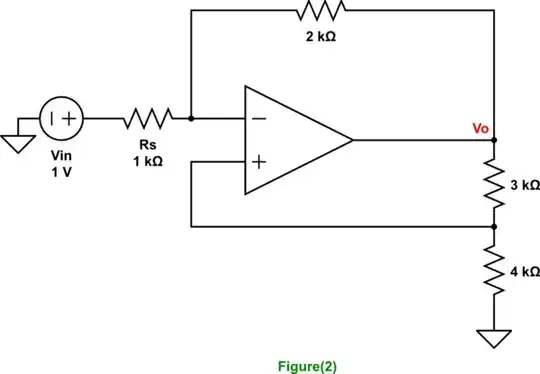
^{simulate this circuit}
then, please explain the type of feedback

Answer 1

You have mis-represented the circuit in the previous question which was given as this:

In the original the input is applied to the non-inverting op-amp input. In your version you connected the input to the inverting input.

If you use an ideal voltage source to provide the input to this circuit, then there is no positive feedback, because the feedback signal is shorted out by the very low resistance of the voltage source.

which is a red flag since inverting-amplifier should have negative gain

The original problem presented a non-inverting amplifier, not an inverting amplifier.

In your version of the circuit, this is indeed a red flag. It shows you you have made a wrong assumption when you assumed the net feedback is negative. In fact in your circuit the net feedback is positive, because the negative feedback signal is shorted by the ideal voltage source.

Answer 2

Both configurations are in use. Both circuits represent a "Negative Impedance Converter" (NIC).

However (for Rf=feedback resistor to the input path, Rx=feedback resistor to the other input and Ro=grounded resistor),

• the first circuit (input at the inverting amplifier) is called "open-circuit stable" and - for stable operation - we require a source resistance RS>RfRo/Rx

• the second circuit (input at the non-inv. input) is called "short-circuit stable" for RS<RfRo/Rx

Application: A combination of both versions leads to a very versatile active block which is always stable (Generalized Impedance Converter, GIC). The NIC (non-inv. input) is used as a basic building block for a non-inverting integrator (DEBOO integrator).