Is it possible to solve for the values of this grid of photoresistors in software?

Question

In this question a circuit was set up as shown:

The idea is to power the rows one at a time, and read off the voltages of each column. But there's a subtle problem. There are alternate paths to ground through other photoresistors, meaning the value of other photoresistors will affect the voltage across the photoresistor you're trying to measure. One solution is to put a diode in series with each photoresistor. I'm wondering if there's a way to solve this in software using math.

After scanning through each column and row in the above circuit, you'll have 12 measurements. There are 12 resistances to determine. Can this system be solved? If so, is it also solvable for an 8x8 grid? Would solving it on an Arduino be feasible?

I've added a review answer to compare the existing three correct answers. I suggest you accept Elliot's answer. — Neil_UK, Dec 18 '20 at 09:10

Neil_UK · Answer 1 · 2020-12-17T15:47:27.893

An alternative to the circuit you have drawn there would be one that's capable of making a guarded measurement. This technique is used extensively in the 'In Circuit' testing industry, for measuring components on boards that are embedded in a network of other components.

The trick is to make the sense inputs virtual grounds, so they sense current, but stay at a known guard potential. This allows the tester to then stimulate the nodes that need to be measured with a high voltage, and to guard the nodes that must not be measured with the guard voltage. This then means that unwanted components have zero voltage across them, so send no current into the measuring sensor.

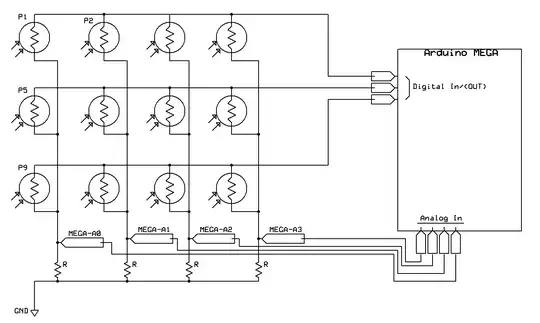
This is the circuit you would use if you wanted to stay with 0 and 5 V rails, obviously this can be extended to any number of rows and columns. You would create Vguard with a simple voltage divider. It does not have to be mid rail, in fact you would have better ADC resolution by setting it to 1 V, so the ADCs could read between 1 V and 5 V. If on the other hand, you were happy to use a negative rail with the sensor amplifiers and then invert their outputs back into the ADC range, then you could do away with R1-3 and OA1-3 and drive the rows directly with the digital outputs, and set Vguard to 0. You have a trade off with whether the extra complexity goes into the row drivers, or the column sensors.

schematic

^{simulate this circuit – Schematic created using CircuitLab}

In operation, the column sensor amplifiers always hold their inputs at Vguard. Start with nothing being measured, the rows drivers all high impedance, so R1-3 take the OA1-3 outputs to Vguard. All the LDR terminals are at Vguard, so no current flows anywhere. Now only one row driver at a time goes low impedance output, taking its row of LDRs to a different voltage. The currents flow through just that row of LDRs into the sense amplifiers, generating a voltage in their feedback resistors.

We refer to driving the other non-measured nodes of the circuit to Vguard as guarding, as it prevents currents circulating around the other components. Note that this technique does not require knowledge of the other circuit components.

There is one limitation with this technique. The amplifier offset voltages limit the dynamic range of the other components that can be handled. For instance, if you're measuring a 1 MΩ resistor with 1 V across it, 1 uA flows. If the next row resistor is 1000 Ω and the guarding amplifier offset is 3 mV, then an unwanted 3 uA flows, completely trashing the accuracy. You need to choose amplifiers to match your error budget. It may be possible with calibration and some extra calculation to compute the corrections for extreme ratio components like this, however amplifiers with offsets in the uV range are available for not too much of a premium over mV offset grades.

This is clever and a useful technique to have. My preference, if feasible, is to solve it in software without extra components, but the alternative is appreciated. — Mike, Dec 18 '20 at 17:46

score 1 · Answer 2 · answered Dec 17 '20 at 07:35

You have 12 measurements for 12 unknowns. This means the set of simultaneous equations is solvable, given one theoretical, and several practical conditions.

a) The matrix formed by [v] = [R][i] should be invertable, that is, non-singular or having a non-zero determinant. You get a singluar matrix when a row or column can be expressed as a linear combination of others. With all photodiodes in the dark, this will be the case. However, that's an uninteresting case and easy enough to spot by using a threshhold. If you have several diodes illuminated, it still may be the case.

b) Noise on the readings could cause the system of equations to become singular, or to make the solution very sensitive to the calculation order. Read up on good methods to invert the matrix.

c) Dynamic range. There are many decades of range between light and dark resistances for photo resistors.

d) There is quite a lot of calculation involved, check whether an Arduino is fast enough, at the precision you will need.

Thanks for the response. I don't have a strong math background, but how would you go about creating these matrices? Is there a method that could be applied to an 8x8 grid? Does it matter that the rows are scanned by setting each of the digital pins to high in sequence, so that the voltages and currents in the circuit are different when we start measuring a new row? — Mike, Dec 17 '20 at 08:09
Thanks for the response. I don't have a strong math background, but how would you go about creating these matrices? *It's tedious* Is there a method that could be applied to an 8x8 grid? *Yes* Does it matter that the rows are scanned by setting each of the digital pins to high in sequence, so that the voltages and currents in the circuit are different when we start measuring a new row? *No, it just gives you different entries in your matrix, whether the 'off' rows are high impedance, or low impedance ground output* — Neil_UK, Dec 17 '20 at 08:54

score 1 · Accepted Answer · answered Dec 17 '20 at 15:50

1

Each column is independent of the other columns, so you just need to worry about three measurements and three unknowns. If you can solve that for one column you can do it for the others. Sounds like just a matter of algebra to me.

answered Dec 17 '20 at 15:50

Elliot Alderson

31,192
5
29
67

So, instead of putting the unused rows in high impedance, we set all rows to ground or 5V, and then the LDRs from other columns can no longer affect the voltage. And we can eliminate the resistors and ground connection at the bottom. That sounds promising. Expanding to 8 rows, there are many possible combinations of row drives. I'm going to have to sit down with some paper to reason about this. – Mike Dec 17 '20 at 21:08
@Mike On 2nd thoughts, you need to keep the resistor at the bottom if you want an absolute measurement of each LDR, without it you can only measure the ratios of the LDRs, which is OK within that column, but not for column to column. Row drives of 001, 010 and 100 should give you 3 equations in 3 unknowns, with the obvious generalisation to 8 or N columns. – Neil_UK Dec 17 '20 at 21:42
Right, of course, without a known resistor value, there's no way to go from measured voltages to absolute resistance. – Mike Dec 18 '20 at 17:34
One possible issue, especially as you increase the number of rows, is the measured voltages become small, decreasing ADC resolution. For example, with 8 rows total and one row driven high, if all LDRs and resistors have the same resistance, the measured voltage would be 1/9th of full voltage. – Mike Dec 18 '20 at 17:43

score 0 · Answer 4 · answered Dec 18 '20 at 09:07

Review

This question already has three correct, but different, answers, each addressing one driving method. It's worth therefore adding this Review Answer, as comments under or additions to any particular answer could get lost.

The three answers differ in how the rows of the photo-resistor matrix are driven. I'll use the particular numbers from the OP of 3 rows, 4 columns.

One row high, other rows high impedance

All the resistors interact, so you have 12 unknowns and 12 measurements. This is soluble in theory, but a matrix that large takes a long time to formulate and to solve, and numerical instabilities could make it very noisy or even insoluble. It does not scale well, an 8x8 array would need solution of a 64x64 matrix, impractical on an Arduino.

One row high, other rows low

Having all row drivers low impedance isolates the columns from each other. Although the photo-resistors interact within the columns, you now have 4 independent sets of 3 measurements of 3 unknowns, a far simpler set of simultaneous equations to solve. It scales well, so even an 8x8 matrix is straightforward.

One row high, other rows to a guard potential

The columns are isolated from one another by the low impedance drivers, but extra hardware is used to isolate the resistors in the row from each other by driving the 'off' rows to a specific potential to eliminate their effect. This eliminates the need to solve any equations, at the expense of the extra hardware. The quality of the hardware affects the dynamic range of values it can handle, so you may or may not be able to 'get away' with very cheap parts.

Conclusion

Comparing all three solutions, and without knowledge of any other constraints faced by the OP, the probable best solution is that of Elliot, all rows driven high or low, with several independent small sets of simultaneous equations to solve.