This opamp has 45 degree phase margin, with Cload of 150 pF.
Assume the Fring is 1MHz (near the UGBW).
To ring at this frequency, with 150pF Cload, the equivalent output inductance is
about 150 microHenries.
However, in your circuit you have 10,000,000 pF Cload or 10uF.
150uH and 10uF resonate at 4,000 Hertz.
Is that 100 ohm into the 10UF adequate dampening?
Z(10uF at 4,000 Hz) = 4 ohms, so that 100 ohm should be good dampening.
On the other hand, this is a VERY NOISY opamp. Figure 17 of datasheet shows 3 microVolts PP in 0.1 to 10Hz region.
And the KT (Nyquist, Boltzmann, Johnson, thermal) noise density is about 30 nanovolts/rtHz. {the internal Rnoise is huge, tho not the worst I've seen; about 50,000 ohms to produce 30 nanoVolts RMS}
In 1MHz, with 30nanoVolts scaled by sqrt(bandwidth), that becomes 30 microVolts RMS, or 200 microVolts PP for 6.2 sigma (aka RMS).
And then a gain of 10. So 2,000 microvolt output PeakPeak (at 1ppm occurrence).
And these diodes cause dead_zone. And the capacitive load.
So I offer this: hang a 1MegOHM from VDD to the Vin-, causing a 3.3 millivolt deadband.
==================================================
After eyeballing your circuit, I realized a certain polarity of Input Offset Voltage would put the opamp into constant ON operation, and the random noise would be amplified.
You can use 3.3 MegOhm, and have only 1 millivolt deadband. That is rather larger than what the datasheet shows for TYPICAL Voffset.
=============================================
Also the electret microphone will have random noise.
And Electret Microphones, usually using a common_source (FET) amplifier with load resistor tied to VDD, HAVE NO PSRR REJECTION.
Make that 2.2K Ohm resistor into two resistors, each 1Kohm, and hang a 100uF from the midpoint of the 2 series resistors.
======================================
Now lets change that 1Mohm/3.3Mohm to 100Kohm, which biases the first_stage input to 30 millivolt, setting the output of the first_stage to 300 millivolt DC.
With that biasing, we should see a nice broadband noise display, with some popcorn or 1/F low frequency spiking superimposed.
How much current is required to abruptly charge a 10uF capacitor by ANY amount of voltage?
=============================
There are FOUR noise sources here
the power supply (we'll ignore that)
the microphone (we'll ignore that)
the broadband noise of the rectifier (amplified 100X [10 * 10])
the broadband noise of the 2nd opamp (amplified only 10X)
If we examine the noise waveforms, we see a
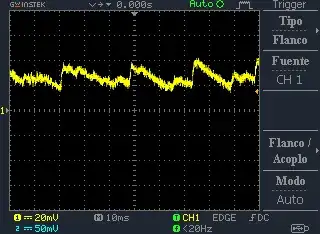
- standard symmetric_swing random noise waveform, with PLUS and MINUS peaks, that is a few milliVolts in peak_peak, because only receives gain from the 2nd stage; this waveform is broadband (there is no bandwidth limitation on this)
and we see
- the rectified and Peak Held waveform, decaying with 0.1 second (10uF and 10ohm) time constant, that is about 10X larger than the symmetric_swing waveform; this waveform is highly limited in the bandwidth, because of the large capacitive load.
So what is going on? These are VERY NOISE OPAMPS. Their Rnoise (my long-time thinking tool for designing at a particular node: identify all the local contributors, model as resistors, and ADD UP THEIR VALUES) is about 50,000 ohms which produces a 30 nanoVolt/rtHz noise density.
As discussed before, 30nV/rtHz in 1,000,000Hz bandwidth becomes 30 microVolts RMS broadband. (I am ignoring how the Gain = 10 will reduce the bandwidth).
And 30 microVolts RMS, in a Gaussian process, becomes 6.2X larger at the 1ppm level, to tell us to expect about 190 microVolts Peak.
Now........... amplify 190 microVolts by (10 * 10) and we expect 19 milliVolts output deviation.
(notice I've not even included the very low frequency noise content of opamps)
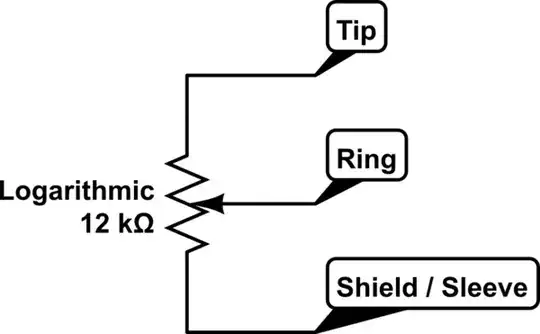
The signal is with almost no noise but sound pressure should be quite high in order to produce something on SOUND_LEVEL.
