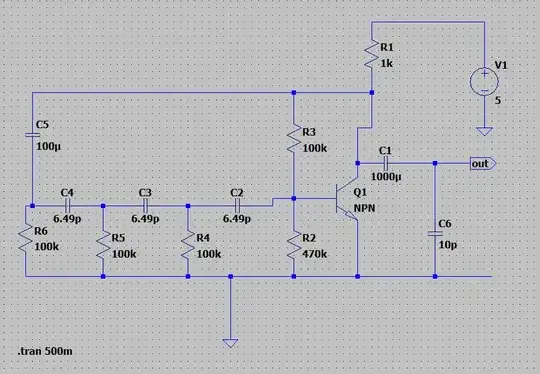
The input resistance of the bipolar is beta * reac, where reac is 1/gm. At Ic = 1mA, reac = 26 ohms. At 0.5mA, reac = 52 ohms.
Your transistor operates at about 2mA, thus reac is 13 ohms.
Scaled by beta, that produces Rin (at DC) of 100 * 13 = 1,300 ohms.
Which in parallel with the final 100K ......... produces problems of phaseshift and attenuation.
Additionally, the input capacitance is set by Miller Multiplication.
That Cin is (1 + gain). Gain is about 1Kohm Rcollector / 1/gm
or 1,000 / 13 == 80X.
With typical bipolars having Cob of 10pF, the Cin is 800pF, not at all appropriate for a 3-stage phase shifter with 7pF.
==================================================
To reduce the input capacitance (to reduce the Miller Multiplication),
introduce a 2nd bipolar atop the first; bias that base to +1 volt, and bypass that (new ) base with 0.1uF because at 100,000Hz the Cob of 10pF? will easily move that base up and down. This (2nd transistor) is called Cascoding.
To improve the Rin, use the ideas suggested in the comments , inserting 10KOhm resistor in the Emitter to Ground. To work with the 100,000 ohm phase shift resistors, you need 1Megohm??? and that requires beta * 100K = 1Meg. This high value of Re requires rethinking all the biasing.
Additionally, the 20pF Cin of the original transistor (reduced from 800pF, as the cascade helps greatly) still is a major problem. 1pF at 1GHz is -j159 ohms;
1pF at 1MHz is -j159,000 ohms; 20pF at 100,000Hz is -j80,000 ohms, so even with
cascading, the Cin will upset the required phaseshifting.
Greatly reduce the Rphase , and greatly increase the Cphase.