I have trouble in understanding the VI graph of the output current (collector current \$I_C\$) in the NPN transistor. More precisely the common base one (this is the first type of transistor I came accross and I don't know if it really makes any difference).
From my understanding the equation \$I_C = \beta_F I_B\$ in only valid in forward active region but not in saturation region. Now the NPN transistor is in saturation region when both the base-emitter and the base-collector regions are forward biased. This means that \$V_{BE} > 0\$ and \$V_{BC} > 0\$. The link between the 3 voltages should be \$V_{CE} = V_{BE} - V_{BC}\$
Since the current are assumed to be all exiting the node, \$I_C\$ is assumed to go from left to right so the voltage arrow go in the opposite direction. The picture above is related to a reverse bias of the p-n region (forward active mode). In that case \$V_{BC}\$ should be negative because as seen in the picture the negative side of the voltage generator is "under the tip" of the voltage arrow.
So here a first question arise:
Are these equations valid ? On what regions can they be used ?
Let's assume that the answer is "yes". I known that \$V_{BE}\$ can be assumed constant and around 0.7 V because this voltage is enough to reduce the depletion region on the n-p side and generate enough \$I_B\$ current. Now what about \$V_{BC}\$ ? According to the formula above \$V_{CE} = V_{BE} - V_{BC}\$ which lend to \$V_{BC} = V_{BE} - V_{CE}\$
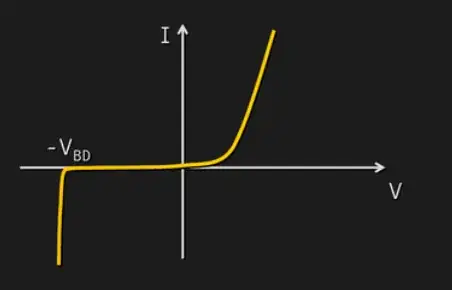
The graph of the VI characteristic of the output current looks like this:
However I can't figure out why the current is creating this "S" shape and why the current form a knee just after the saturation region. The only thing that comes in my mind is the graph of the VI characteristic of a generic PN-junction:
However this doesn't fit well with the formula when I try to see the V in the graph as \$V_{BC}\$.
What am I missing ? Is there a formula to explain this shape of the VI characteristic of the NPN transistor ?