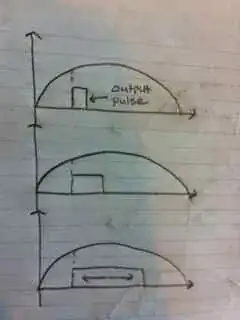
I am trying to prove Theorem 6.2 on page 127 of the book Real-Time Systems by Jane W. S. Liu:
http://www.cse.hcmut.edu.vn/~thai/books/2000%20_%20Liu-%20Real%20Time%20Systems.pdf
It is based on Early Deadline First(EDF) scheduling.
It says on the book that the proof is similar to the proof for Theorem 6.1 on page 124-126. However, I am still stuck.
Here is what I have so far: