I'm asked to find the order, type, number of poles and zeroes and the dc gain of the following filter:
Since the output of each integrator is the input both of the following and the preceding integrators, this filter is a leapfrog filter. In particular, I know from the theory that it is a low-pass filter implementing an all-pole low-pass ladder. As a consequence, there are no zeroes. The number of poles (and thus the order of the filter) is given by the number of integrators: 4.
I then have this equivalent circuit:
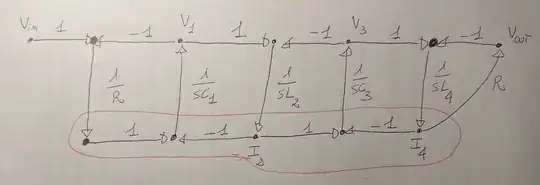
Now, I draw the corresponding flowgraph:
Considering the red loop, then by multiplying all the incoming branches by R and dividing all the outcoming branches by R, I can transform the currents into voltages. In particular, the state variables I2 and I4 become V2' and V4', respectively.
Question: is there an error in the exercise? Indeed, if you consider for example the output of the second integrator V2':
- according to my flowgraph, V2' should go directly (+1) as input of the following integrator, and should be swapped (-1) at the input of the preceding integrator;
- according to the exercise scheme, V2' gets swapped at the input of the following integrator, and goes directly (without swapping) at the input of the preceding integrator.