Bird's Eye View of Single-Ended and Bridge-Tied Output Loads
Start with the speaker itself and assume at first that you have access to a bipolar power supply rails, such as \$\pm12\:\text{V}\$. Let's also assume that you have a ground-referenced input signal. Then there are two basic arrangements:
simulate this circuit – Schematic created using CircuitLab
(Keep in mind that it is possible to also use an audio transformer to match up the load, better. So the speaker, as shown, could be replaced by the primary of an audio transformer with the speaker hooked up to the secondary.)
I'm showing everything hooked up as DC connections, above, and the AMP is assumed to have some possible voltage gain, as well. There is a lot buried inside the AMP.
If the input is at \$0\:\text{V}\$ then the output will also be \$0\:\text{V}\$, for both the single-ended and the bridge-tied load arrangements.
The inverter shown for the bridge-tied load arrangement is designed to mirror the voltage across the ground reference, so that if \$\text{IN}_1=+10\:\text{mV}\$ then the inverter output will be \$-10\:\text{mV}\$. (I used "180" on the symbol to suggest the idea of \$180^\circ\$ phase relationship between its input and output.)
In the single-ended case, the bipolar rail voltages for the amplifier must be \$V=\sqrt{2\cdot R\cdot P}\$, where \$P\$ is the desired maximum power output, \$R\$ is the speaker impedance, and \$V\$ is the magnitude of each of the two bipolar rails. You must pad \$V\$ a little bit to account for the control overhead voltage, which is typically on the order of about \$1\:\text{V}\to 2\:\text{V}\$ for each rail.
For example, if you have \$R=8\:\Omega\$ and \$P=1\:\text{W}\$ then expect \$V=\sqrt{2\cdot 8\:\Omega\cdot 1\:\text{W}}=4\:\text{V}\$. Given the lower end of about \$1\:\text{V}\$ overhead, this would suggest bipolar power supply rails of \$\pm 5\:\text{V}\$.
There is a huge advantage for the bridge-tied load. In this case, you'd only need one of the rails -- namely, \$+5\:\text{V}\$. So you save yourself an entire voltage rail! Take a look at the TDA8551: 1 W BTL audio amplifier with digital volume control datasheet for an example proving exactly this result. Here all you need is a single supply rail of \$5\:\text{V}\$ in order to deliver \$1\:\text{W}\$ into a speaker load of \$8\:\Omega\$! (They achieve this by allowing each amplifier to go into gentle saturation as they approach their rails, without significant distortion.)
The problem with bridge-tied loads (BTL), of course, is that they require two amplifiers. Not just one. (And an analog inverter.)
Single-Supply Rail Case
Let's assume you aren't in a position to create two amplifiers (plus an inverter) in order to get the most out of a single supply rail. But that you are stuck with a single supply rail.
Here, you can make an adjustment to the earlier diagram:
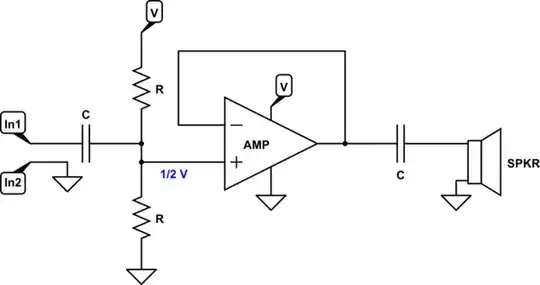
simulate this circuit
Here, if both \$R\$ values are the same, then the midpoint is half-way between the supply voltage and ground. Now, the amplifier output will also be, nominally, half-way between the supply voltage and ground. The two capacitors will charge up to the difference, quickly, adding just enough voltage on both ends of the system so that the quiescent state will be just fine and there will be no current in the speaker without an input signal change.
We are still limited by the need for a \$1\:\text{V}\to 2\:\text{V}\$ voltage overhead. But at least we can operate the system now with a single voltage rail.
Let's assume your \$R=4\:\Omega\$ and \$V=12\:\text{V}\$. In this case, we find that \$2\:\text{W} \le P\le 3.125\:\text{W}\$, after subtracting the voltage overhead range. This won't be between your hope of \$20\:\text{W}\to 30\:\text{W}\$. But it's something.
Jump Right In
With BJTs, you may consider about \$2\:\text{V}\$ of voltage headroom. This leaves about \$12\:\text{V}-2\cdot 2\:\text{V}=8\:\text{V}_\text{PP}\$ or \$4\:\text{V}_\text{PK}\$. From that, we can estimate a maximum of about \$\frac{\left(4\:\text{V}_\text{PK}\right)^2}{2\;\cdot\; 4\:\Omega}=2\:\text{W}\$ into your \$4\:\Omega\$ speaker. I don't think you can expect more than this from your \$12\:\text{V}\$ rail voltage.
It's pretty easy to see that your peak current will be \$1\:\text{A}_\text{PK}\$. At that current, you cannot just use a small-signal BJT. In fact, you probably will require at least two BJTs for each quadrant. So your output stage will have four BJTs in it.
(We could do better with a bridge-tied load. But that's a lot more work.)
You can use either Sziklai or Darlington pairs for this. I'd recommend Sziklai, to help reduce the overhead voltage required. (In fact, you must use Sziklai if you want to keep the overhead voltage to around \$2\:\text{V}\$ at each margin.) So I think it's a requirement for Sziklai, in this case.
In general, something like this:
simulate this circuit
There's a need here for a special voltage difference (\$V_\text{SPAN}\$) which can be a \$V_\text{BE}\$-multiplier construction. If so, there will be a need for a current source to feed it, as well.
For the output, there may need to be a Zobel network (not shown.) But that can also be deferred until later.
That said, the basic idea for the 2-quadrant driver is represented above. And it provides a starting point for designing the rest. And now you can also easily see why there is some overhead voltage required, too.
I've made some points, now. I think you can now see that there is more required, than the approach you provided. These details are important. You've also now (hopefully) realize that with a \$12\:\text{V}\$ single-rail supply you can only expect about \$2\:\text{W}\$ (and likely no more than \$2.5\:\text{W}\$ unless you go to some extreme measures) into a \$4\:\Omega\$ speaker. This is simply because you have to take into account the overhead voltages required, both on the near-ground side as well as the near-\$V_\text{CC}\$ side, for controlling the output. With only a \$12\:\text{V}\$ single-rail supply, these subtractions really hurt a lot as they are a significant part of the total supply range.
I'm tired at this point. It's enough to make the case that you cannot expect much more than about \$2\:\text{W}\$ into a \$4\:\Omega\$ speaker with a single \$12\:\text{V}\$ supply, unless you use a bridge-tied arrangement (which is more than twice as complex to develop.)