I am trying to find the transfer function of the common gate transimpedance amplifier. The transfer function that I got is different than the one at the original publication even though it leads to the same DC gain. There is no derivation in the publication, only final result, as I copied in my post below. So, I think it is just fine not reading the original manuscript.
I am aware that the transfer function can be different depending on the assumption used. looking at the result from the publication, it does not ignore \$ r_{o} \$.
Am I missing something here?
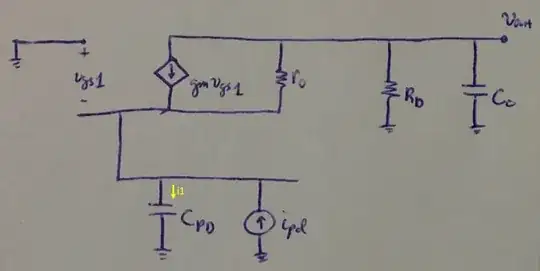
This is the diagram:
From observation: $$ v_{s1} = \frac{1}{sC_{PD}}i_{1} $$ $$ v_{out} = \left(R_{D} || \frac{1}{sC_o} \right) (i_{pd} - i_{1}) $$ $$ i_{1} = i_{pd} - \frac{v_{out}}{\frac{R_{D}}{sC_{o}R_{D}+1}} $$ $$ \left( v_{s1} - v_{out} \right) = (i_{pd} - i_{1} + g_{m}v_{gs1})r_{o} $$ $$ v_{gs1} = \left(0 - \frac{1}{sC_{PD}}i_{1} \right) $$
From equations above, we can solve for \$ v_{out}/i_{pd} \$ by eliminating \$ v_{s1}, v_{gs1}, i_{1} \$.
Two checkpoints are written here:
$$ \frac{1}{sC_{PD}}i_{1} - v_{out} = \left[ i_{pd} - \left( i_{pd} - \frac{v_{out}}{\frac{R_{D}}{sC_{o}R_{D}+1}} \right) +g_{m} \left( - \frac{1}{sC_{PD}}i_{1} \right) \right] r_{o} $$
$$ v_{out} \left(1 + \frac{(sC_{o}R_{D} + 1)r_{o}}{R_{D}} \right) = \left( \frac{1}{sC_{PD}} + g_{m} \frac{1}{sC_{PD}}r_{o} \right) \left( i_{pd} - \frac{v_{out}}{\frac{R_{D}}{sC_{o}R_{D}+1}} \right) $$
At the end, I got this:
$$ \frac{v_{out}}{i_{pd}} = \frac{(1 + g_{m}r_{o})R_{D}} {sC_{PD}R_{D} + \left[ (sC_{o}R_{D} + 1)(sC_{PD}r_{o} + g_{m}r_{o} +1 ) \right] }$$
From the publication, this is the transfer function: